Kezdőlap


Feladat:	F.2161	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Balogh S. , Benkó B. , Bertóti E. , Bogdán Klára , Botta Melinda , Bukta Gy. , Bölcsföldi L. , Cseri I. , Csirke Zs. , Dénes L. , Erdélyi T. , Fodor L. , Fülöp Veronika , Inacsovszky Judit , Király E. , Kőrössy Katalin , Kovács G. , Laszip F. , Lendvai J. , Liszkay L. , Molnár Emese , Németh K. , Pátkai Andrea , Pintér F. , Schwarcz P. , Szegedy P. , Szekeres G. , Szőke S. , Tulipán Gy. , Varga J. , Varga Lívia , Winkler R. , Zakar L.
Füzet:	1979/január, 10 - 12. oldal		PDF \| MathML
Témakör(ök):	Beírt alakzatok, Feladat
Hivatkozás(ok):	Feladatok: 1978/szeptember: F.2161

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Azt fogjuk bizonyítani, hogy a $B C D$ szög felezőjének az $A D$ szakasszal való $K$ metszéspontját $B$ -vel összekötve, ez az egyenes felezi az $A B C$ szöget. Ebből már következik, hogy $K$ egyenlő távolságra van a $D C, C B$ , valamint $A B$ oldaltól, és mivel a hatszög szimmetrikus $A D$ -re mint tengelyre, azért $K$ a $D E$ , $E F$ és $F A$ oldaltól is egyenlő távolságra van; így pedig a $K$ körüli, $A B$ -t érintő kör a hatszögnek mind a hat oldalát érinti.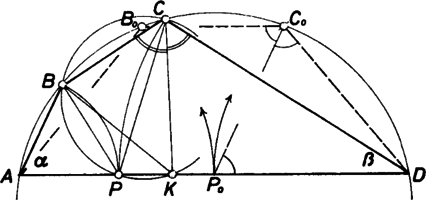

A B C D

konvex húrnégyszögre vonatkozó állításunk akkor is helyes, ha

A D

a körnek tetszőleges húrja; ezért nem fogjuk felhasználni, hogy

A D

átmérő.

P

-nek abban a

P_{0}

helyzetében, amelyre

A P_{0} = P_{0} D

, az

A D C_{0} B_{0}

húrnégyszög szimmetrikus trapéz,

C_{0} B_{0} ∥ D A

, és

K_{0}

azonos

P_{0}

-lal, hiszen

D C = D P

alapján

D C_{0} P_{0} ∢ = D P_{0} C_{0} ∢ = B_{0} C_{0} P_{0} ∢

, és a szimmetria alapján

K_{0} B_{0}

is felezi az

A B_{0} C_{0}

szöget, amint állítjuk.
Most már az általánosság csorbítása nélkül föltehetjük, hogy

A P < P D

(más szóval: hogy a húrnak

P

-hez közelebbi végpontját jelöltük

A

-val). Így nyilván

\begin{matrix} α = B A D ∢ > B_{0} D A ∢ = C_{0} D A ∢ > C D A ∢ = β . \end{matrix}

C

-nél levő szög felezője

A D

-t a

P D

szakasz belsejében levő

K

-ban metszi, mert az ábra szerint, a forgásszögeket a

C P

alapiránytól mérve

\begin{matrix} P C K ∢ = P C D ∢ - K C D ∢ = \frac{1}{2} (180^{\circ} - β) - \frac{1}{2} B C D ∢ = \\ = \frac{1}{2} (180^{\circ} - β) - \frac{1}{2} (180^{\circ} - α) = \frac{1}{2} (α - β) > 0^{\circ} . \end{matrix}

Eszerint

P

B K

egyenesnek

C

-t nem tartalmazó partján van.
A

B K

szakasznak

C

-ből és

P

-ből vett látószögeire viszont

A B = A P

alapján fennáll

\begin{matrix} B C K ∢ = \frac{1}{2} B C D ∢ = \frac{1}{2} (180^{\circ} - B A D ∢) = B P A ∢ = 180^{\circ} - K P B ∢, \end{matrix}

vagyis

K

C

B

P

ebben a sorrendben egy kör pontjai. Így pedig az előbbi számítás felhasználásával

\begin{matrix} A B K ∢ = A B P ∢ + P B K ∢ = \frac{1}{2} (180^{\circ} - α) + P C K ∢ = \frac{1}{2} (180^{\circ} - β) = \frac{1}{2} A B C ∢ . \end{matrix}

Ezzel a kiindulásul kimondott állításunkat bebizonyítottuk.

Megjegyzések. 1. Sok téves dolgozat született a következő megfontolás alapján: ,,Ha egy hatszögbe kör írható, akkor ‐ mint egyszerűen belátható ‐ 3‐3 nem szomszédos oldala hosszainak összege megegyezik. Már pedig ez teljesül a kérdéses hatszögben.'' Ámde ez az egyenlőség csak következmény, csak szükséges, de nem elégséges feltétele annak, hogy a hatszögbe kört lehessen írni. Kör köré írt négyszögre a megfordítás is igaz, de az iskolai anyagban ez sem kerül bizonyításra.
2. Mások félreértése az volt, hogy a H. S. M. Coxeter‐S. L. Greitzer: Az újra felfedezett geometria c. könyv 127. oldalán olvasható tételben ‐ ,,ha egy hatszög három átlója egy ponton megy át, akkor a hat oldal érinti ugyanazt a kúpszeletet, ...'' ‐ kúpszeletként csak körre gondoltak. ‐ Mindkét téves hivatkozásra ellenpélda, ha egy helyes ábrának merőleges affin képeit vesszük

A D

-re mint tengelyre, egymás után két különböző

λ

arányszám mellett.
3. Körülírt és beírt körrel egyaránt bíró sokszöget bicentrikusnak (két középpontúnak) szokás mondani. Az ilyenekben ‐ a háromszögben ismert Euler-féle relációhoz hasonlóan ‐ ismeretes néhány összefüggés az

r

és

ϱ

sugarak és a középpontok

d

távolsága között (esetünkben

2 d = K D - K A

):
3-szögben

d^{2} = r^{2} - 2 r ϱ

;
4-szögben

2 ϱ^{2} (r^{2} + d^{2}) = {(r^{2} - d^{2})}^{2}

;
5-szögben

ϱ (r - d) = (r + d) (\sqrt[]{{(r - ϱ)}^{2} - d^{2}} + \sqrt[]{2 r (r - ϱ - d)})

;
6-szögben

3 {(r^{2} - d^{2})}^{4} = 4 ϱ^{2} (r^{2} + d^{2}) {(r^{2} - d^{2})}^{2} + 16 r^{2} ϱ^{4} d^{2}