Kezdőlap


Feladat:	F.2144	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1978/szeptember, 11 - 12. oldal		PDF \| MathML
Témakör(ök):	Szélsőérték differenciálszámítással, Téglatest, Feladat
Hivatkozás(ok):	Feladatok: 1978/március: F.2144

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A téglatest szimmetriái alapján a kérdéses összeg négy tagja egyenlő, továbbá $X Y = 2 G X$ , így elég vizsgálnunk az $f (x) = G X + 2 X A$ függvénynek (az összeg felének) változását, ha $G X = x$ a $[0, G E]$ intervallumban változik. Legyen $A B = 2 b$ és $A E = e$ , így

\begin{matrix} f (x) = x + 2 \sqrt[]{{(b - x)}^{2} + e^{2}} . \end{matrix}

Deriváltja eltűnésének feltétele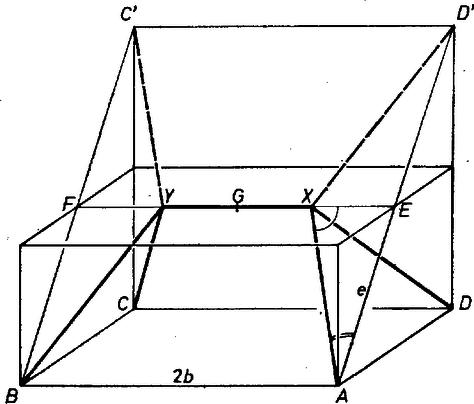

\begin{matrix} f' (x) = 1 - \frac{2 (b - x)}{\sqrt[]{{(b - x)}^{2} + e^{2}}} = 1 - \frac{2 \cdot X E}{X A} = 0, \end{matrix}

vagyis

\begin{matrix} \frac{X E}{X A} = cos E X A ∢ = \frac{1}{2}, E X A ∢ = 60^{\circ} . \end{matrix}

Ez akkor és csak akkor teljesül, ha ‐ visszatérve a változó használatára és figyelembe véve a mondott értelmezési tartományt ‐

\begin{matrix} \frac{b - x}{\sqrt[]{{(b - x)}^{2} + e^{2}}} = \frac{1}{2}, x = b - \frac{e}{\sqrt[]{3}} ≧ 0, b ≧ \frac{e}{\sqrt[]{3}}; \end{matrix}

szavakban: ha a

G E A

síkban

A E

-vel

30^{\circ}

-os szöget bezáró egyenes a fedőlap középvonalát

E

és

G

közötti

X

pontban metszi, függvényünknek csak ebben az esetben lehet szélső értéke az intervallum belsejében, illetve éppen

G

-ben.

Mindenesetre

f' (b) = 1 > 0

. Ha

X

G E

szakasz belsejében keletkezett, akkor

E G A ∢ < E X A ∢ = 60^{\circ}

, és így

\begin{matrix} f' (0) = 1 - \frac{2 b}{\sqrt[]{b^{2} + e^{2}}} = 1 - 2 \frac{G E}{G A} = 1 - 2 cos E G A ∢ < 0, \end{matrix}

tehát

f' (x)

az intervallumban növekvő, negatívból pozitívba megy át, és így

f (x)

-nek minimuma van a talált helyen. Ha pedig az

f' (x) = 0

-t adó helyre

x < 0

, és ide értve

x = 0

-t is, akkor

f (x)

[0, G E]

intervallumban növekedő, tehát minimuma

x = 0

mellett van, amikor

X

azonos

G

-vel.

Megjegyzések. 1. Ismert síkbeli feladatba megy át

2 \cdot A X + X G

minimumának a kérdése, ha

D

helyett a fedőlap síkjára való

D'

tükörképét vesszük, másrészt egyelőre nem korlátozzuk

X

-et az

E F

egyenesre, csak az

A G D'

háromszög síkjára. Ismeretes, hogy így az

X A + X G + X D'

összeg a háromszög ún. izogonális (magyarul: egyező látószögű) pontjára a legkisebb, amelyből az

A X G

G X D'

és

D' X A

látószögek közös értéke

120^{\circ}

. Ez a pont azonban csak akkor létezik, ha a háromszög egyik szöge sem nagyobb

120^{\circ}

-nál; ha viszont van ilyen szög, akkor annak a csúcsára minimális az összeg és a látószögek ilyenkor nem egyenlők. ‐ Esetünkben

G A = G D'

miatt csak

G

-ben lehet szó ilyen szögről, éppen ennek esetét zárta ki (emelte ki) a megoldás. ‐ Az

A G D'

háromszög tengelyes szimmetriája alapján az izogonális (régebbi nevén: Torricelli-féle) pont az

E G

magasságra esik.
2. Visszatérve az eredeti feladatra, kérdésünk rokonságban áll az

A

B

C'

D'

(egy síkbeli) pontok közti minimális összhosszúságú úthálózat kérdésével (lásd a P.20. problémát, K. M. L. 39 (1969) 215. old., továbbá speciális esetre a Gy. 1317. gyakorlatot, 44 (1972) 112. old.).
3. Könnyen adódik az a sejtés, hogy ha az

E F

középvonalon nem találtunk

X

(és

Y

) pontot, akkor a fedőlap

A D

-vel párhuzamos középvonalán lesz megfelelő pont.
4. A feladat tekinthető a következő (egyszerűsített) gyakorlati probléma részének: két egymásra merőleges irányú (különböző szélességű) csatorna egy várost 4 részre tagol. Olyan gyaloghidat kívánunk a keresztezés fölött lépcsőfeljárókkal, amely a város bármely két része közt összeköttetést létesít. (Magasságát a hajózás szabja meg. Ekkor persze a lépcsők meredeksége is figyelembe veendő.)