Feladat:	F.2142	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1978/október, 61 - 62. oldal		PDF  |  MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenlőtlenségek, Koszinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1978/március: F.2142

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.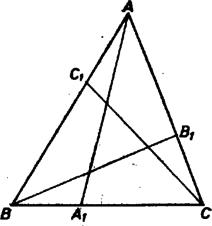     Jelöljük a $B{A}_1:BC$ arány értékét $\lambda$-val $\left(0<\lambda <1\right)$. A cosinus tételnek az $A{A}_1$ és $AC=b$ szakaszokra való alkalmazásával, a háromszögben szokásos jelölésekkel $\begin{array}{c}{\displaystyle A{A}_1^2=c^2+{\lambda }^2{a}^2+\lambda \left(-2ac\text{cos}\beta \right)=c^2+{\lambda }^2{a}^2+\lambda \left(b^2-a^2-c^2\right)\mathrm{.}}\end{array}$ (1) alapján az is igaz, hogy $C{B}_1:CA=A{C}_1:AB=\lambda$, hiszen az arányok közös értéke $\mu =\lambda :\left(1-\lambda \right)$ (és ez $>0$, innen egyértelműen $\lambda =\mu \left(1+\mu \right)$. Ennélfogva hasonlóan ${\displaystyle \begin{array}{c}\hfill {\displaystyle B{B}_1^2=a^2+{\lambda }^2{b}^2+\lambda \left(c^2-b^2-a^2\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle C{C}_1^2=b^2+{\lambda }^2{c}^2+\lambda \left(a^2-c^2-b^2\right)\mathrm{,}}\hfill \end{array}}$ így a vizsgálandó, a (2) közepén álló összeg: $\begin{array}{c}{\displaystyle A{A}_1^2+B{B}_1^2+C{C}_1^2=\left(1-\lambda +{\lambda }^2\right)\left(a^2+b^2+c^2\right)\mathrm{,}}\end{array}$ és ezt beírva, $a^2+b^2+c^2>0$ figyelembevételével elég bizonyítani az osztással adódó, az eredetivel ekvivalens $\begin{array}{c}{\displaystyle \frac{3}{4}\leqq 1-\lambda +{\lambda }^2<1}\end{array}$ kettős egyenlőtlenséget. A középső kifejezést a jobb oldali számból, valamint a középsőből a bal oldali számot kivonva, egyaránt nem negatív kifejezést kapunk, ezzel bebizonyítottuk a feladat állítását: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \lambda -{\lambda }^2=\lambda \left(1-\lambda \right)>\mathrm{0,}}\hfill \\ \hfill {\displaystyle {\lambda }^2-\lambda +\frac{1}{4}={\left(\lambda -\frac{1}{2}\right)}^2\geqq 0.}\hfill \end{array}}$ Pontosabban megnézve azt kaptuk, hogy (2) első egyenlőtlenségében akkor és csak akkor teljesül egyenlőség, ha $\lambda =1/2$, vagyis az $A{A}_1\mathrm{,}B{B}_1\mathrm{,}C{C}_1$ szakaszok a háromszög súly vonalai (tehát négyzetösszegük egyenlő az oldalak négyzetösszegének $3/4$-szeresével). Továbbá (2) második egyenlőtlenségében nem teljesül egyenlőség, amíg $A_1\mathrm{,}{B}_1\mathrm{,}{C}_1$ az oldalak (azaz oldalszakaszok) belső pontjai. (Az viszont semmitmondó, hogy $\lambda =0$, ill. 1 esetén egyenlőség áll, a két kifejezés csak jelölésben különbözik.) Azt is látjuk, hogy $\lambda >1$ esetén ($A_1\mathrm{,}\text{...}$ a meghosszabbításokon) már nem érvényes (2) jobb oldali egyenlőtlensége.