Feladat: F.2136 Korcsoport: 14-15 Nehézségi fok: átlagos
Füzet: 1978/november, 123 - 124. oldal  PDF  |  MathML 
Témakör(ök): Kombinatorikus geometria síkban, Logikai feladatok, Feladat
Hivatkozás(ok):Feladatok: 1978/február: F.2136

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a pálya sarkait A, B, C, D-vel, közülük A legyen az, ahonnan a játékvezető indul. Ha A-ból nem látja a sípot, induljon a játékvezető a szemközti C sarok felé. Mindaddig menjen az AC mentén egyenesen előre, amíg meg nem látja a sípot vagy azt nem mondják neki, hogy az utolsó lépésével távolodott tőle. Az utóbbi esetben jelöljük az utolsó lépés kezdőpontját P-vel, végpontját Q-val. Térjen vissza most a játékvezető Q-ból P-be, és innen az AC egyenesre merőlegesen lépjen egyet. Ha ezzel közelebb jut a sípjához, menjen tovább egyenesen mindaddig, amíg azt meg nem látja. Különben az AC egyenesre merőleges egyenesen az ellenkező irányba menjen mindaddig, amíg meg nem látja a sípot.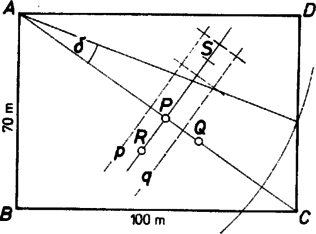

 
 

Ha a játékvezető az AC egyenesen haladva látja meg a sípot, nyilvánvalóan legfeljebb [d+1]-et lép. (Szokás szerint [x]-szel a legnagyobb, x-nél nem nagyobb egész számot jelöljük.) Különben legyen q a PQ szakasz felező merőlegese, és p a q-nak P-re vonatkozó tükörképe. Mivel Q-ba lépve a játékvezető távolodott a síptól, az a q-nak P-t tartalmazó oldalán van. Mivel utoljára P-be lépve nem távolodott a síptól, a síp p-nek is a P-t tartalmazó oldalán van, tehát benne van a p, q egyenesek által határolt sávban. Jelöljük az AC-re merőlegesen tett első lépés végpontját R-rel. Ha ezzel közelebb jut a játékvezető a síphoz, a síp az AC egyenes R-t tartalmazó oldalán van, különben az ellentétes oldalon kell lennie. Akárhogy is van, a sáv közepén haladva a játékvezető nem mehet el a síp mellett anélkül, hogy meg ne látná, hiszen a középvonaltól a sáv határai fél méterre vannak, ő pedig 1 méterről észreveszi a fűben a sípot. Ha mondjuk S-be lépett utoljára, és onnan látta meg a sípot, akkor egyrészt AS≤d+1, másrészt AP+PS≤AS⋅2, aminél a szükséges lépések száma legfeljebb 4-gyel több. (Két lépést jelent a Q-ból való visszafordulás, amihez újabb két lépés járul, ha R-ből is vissza kell fordulnia.) Tehát a játékvezető legfeljebb [2(d+1)]+4 lépéssel megtalálja a sípját.
 

Megjegyzés. Tekintsük az A középpontú, d sugarú körnek az ABCD téglalapba eső darabját. Vágjuk ezt ketté az AC egyenessel, és jelöljük a nagyobb darabhoz tartozó középponti szöget δ-val. Ha δ<45∘, a fenti becslésben 2 helyére a nála kisebb (cosδ+sinδ) írható. Így ha d>100, a fenti stratégia mellett általában kevesebbet kell lépnie a játékvezetőnek, mintha A-ból D felé indulna, majd az AD-re merőleges egyenes mentén folytatná a keresést. Nevezetesen, ha d=AC, a mi stratégiánk mellett 122 lépés elég, AD mentén indulva pedig 170 lépés kell. Jelöljük általában L(T)-vel egy tetszőleges stratégia esetén a szükséges lépések számát, ha a sípot T-ben találja meg a játékvezető, és legyen M(d) az L(T) számok maximuma azokon a T pontokon, amelyekre AT=d. Legyen m(d) az M(d) számok minimuma az összes lehetséges stratégián. Ennek az m(d) függvénynek csak d=AC mellett határoztuk meg az értékét, a teljes függvény meghatározása igen nehéz feladat.
Ha d nem túl kicsi, előnyösebb, ha a játékvezető mindenféle irányban tesz egy-egy kutató lépést, és az ezekre kapott válaszok alapján indul el a síp felé. Vizsgálható a feladat végtelen nagy pályán is. Igen nehéz kérdésnek látszik azt eldönteni, hogy található-e olyan K szám és olyan stratégia, amely mellett tetszőleges nagy d mellett elegendő [d+K] lépés a síp megtalálásához.