Feladat: F.2132 Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1978/május, 202 - 204. oldal  PDF  |  MathML 
Témakör(ök): Négyszög alapú gúlák, Paralelogrammák, Térelemek és részeik, Térgeometriai bizonyítások, Feladat
Hivatkozás(ok):Feladatok: 1978/január: F.2132

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a gúla alaplapja az ABCD négyszög, csúcspontja E. Így olyan sík létezését kell megmutatnunk, amely párhuzamos egyenesekben metszi egyrészt az ABE, CDE oldallappárt, másrészt az ADE, BCE lappárt. Egy S sík akkor és csak akkor metsz párhuzamos egyenesekben két (egymást E-ben metsző) síkot, ha párhuzamos azok metszésvonalával.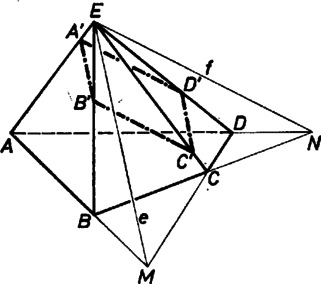

 

 

1. ábra

Legyen az ABE és CDE síkok metszésvonala e, a BCE és az ADE síkoké, f , az e és f által kifeszített sík legyen S0 (1. ábra). Az e metszésvonal átmegy az alapsíknak azon az M pontján, ahol az AB, CD alapélek egyenesei metszik egymást. Mivel az alapnégyszög konvex, M kívül van rajta, és ugyanígy az AD, BC egyenesek metszéspontja is, az az N, ahol f metszi az alapsíkot. Eszerint az alapidom és vele az egész gúla is S0-nak egyik félterében van. (Ha M, ill. N nem létezik, mert AB∥CD, ill. AD∥BC, akkor e, ill. f párhuzamos az alapsíkkal.) S0-nak csak egy közös pontja van a gúlával, E; így S0-t párhuzamosan eltolva az alap felé, a keletkező S az AE, BE, CE, DE oldaléleket rendre olyan A', B', C', D' pontokban metszi, hogy A'B'∥e∥C'D' és A'D'∥f∥B'C', tehát A'B'C'D' paralelogramma. Addig tolhatjuk S-et, míg eléri az alapnégyszögnek S0-hoz legközelebbi csúcsát.
 (R. Zs.)
 

Megjegyzések. 1. A fenti bizonyításban a paralelogrammának azt a (definiáló) tulajdonságát használtuk fel, hogy mindkét pár szemben fekvő oldala párhuzamos. Ha viszont erre az (ugyancsak definiáló) tulajdonságra kívánunk támaszkodni: valamelyik szemben levő oldalpár párhuzamos és egyenlő hosszú, akkor elegendő meghatároznunk a fenti e és f metszésvonalak egyikét, mondjuk e-t. Vegyünk ezután egy-egy, e-vel párhuzamos szakaszt az ABE és CDE háromszögben: A*B*-ot, ill. C*D*-ot. Ha C*D*=A*B*, akkor készen is vagyunk, az A*B*C* sík paralelogrammában metszi a gúlát. Az ellentétes esetben vehetjük a jelölést úgy, hogy C*D*>A*B*, és vegyük C*D* helyett azt a vele párhuzamos C'D' szakaszt, amely egyenlő A*B*-gal. Ez szintén benne van a CDE lapban és az A*B*C' sík megfelel az állításnak (2. ábra).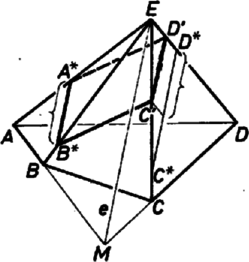
 

 

2. ábra
Mindjárt itt célszerű kimondani összehasonlításul: a II. megoldás erre támaszkodik: a paralelogramma centrálisan szimmetrikus négyszög.
2. Ha a megoldásbeli M és N pontok egyike sem jön létre (e, ill. f könnyű kijelölése céljára), akkor az alapidom már eleve paralelogramma és minden olyan sík megfelel, amely vele párhuzamos és nála közelebb van E-hez ugyanebben a féltérben, (más sík pedig nem felel meg).
3. Megoldásaink kissé szerkesztés jellegűek, az eltérés csak az, hogy végtelen sok megoldásuk van.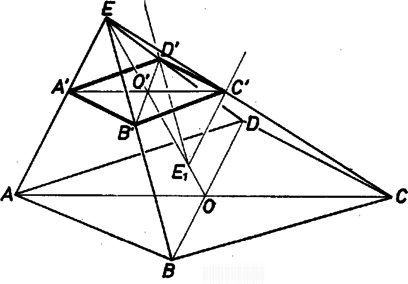
 

 

3. ábra

II. megoldás. Az előbbi jelölések mellett tegyük fel, hogy találtunk egy S síkot, amely a gúla palástját az A'B'C'D' paralelogrammában metszi (3. ábra). Legyen az ABCD négyszög átlóinak metszéspontja O. Az A'B'C'D' paralelogramma átlóinak O' metszéspontja rajta van az EAC és EBD síkok metszésvonalának a gúlába eső szakaszán, vagyis OE-n. A paralelogramma centrálisan szimmetrikus O'-re, így az AE élt O'-re tükrözve; a tükörkép C'-ben metszi CE-t, a BE élt O'-re tükrözve, a tükörkép D'-ben metszi DE-t, végül C' és D'-nek O'-ra vonatkozó tükörképe éppen A', illetve B'. (Az ábrán E tükörképe 0'-re E1.)
Mivel ABCD konvexsége miatt OE a gúla belsejében halad, megválasztható OE-n egy O' pont úgy, hogy a fenti tükrözéseket elvégezve, A', B', C', D' pontok a gúla oldalszakaszaira essenek. Könnyű belátni, hogy ez az eset következik be, ha O'E≤O'O. A fenti meggondolás alapján nyilvánvaló, hogy A'B'C'D' paralelogramma, vagyis A'B'C'D' síkja a gúla palástját éppen az A'B'C'D' paralelogrammában metszi.