Kezdőlap


Feladat:	F.2125	Korcsoport: 16-17	Nehézségi fok: -
Füzet:	1978/április, 155 - 156. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Beírt gömb, Négyszög alapú gúlák, Szélsőérték-feladatok differenciálszámítás nélkül, Térgeometriai számítások trigonometria nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1977/december: F.2125

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az alap csúcsait $A$ , $B$ , $C$ , $D$ -vel, középpontját $T$ -vel, a gúla ötödik csúcsát $E$ -vel, a beírt gömböt $G_{0}$ -lal, középpontját $O$ -val, a körülírt gömböt $G$ -vel, középpontját $K$ -val. Mivel a gúla egyenes, és alapja szabályos sokszög, $O$ és $K$ rajta van az $E T$ egyenesen. Emellett $K$ -t egyértelműen meghatározza az, hogy $G$ átmegy az $A$ , $C$ , $E$ pontokon. Jelöljük a $B C$ , $D A$ szakaszok felezőpontját $U$ -val, $V$ -vel. Mivel a gúla szimmetrikus az $U V E$ síkra, $G_{0}$ az $U V E$ háromszög oldalain érinti az oldalakat tartalmazó lapokat. Más szóval $G_{0}$ -ból az $U V E$ sík az $U V E$ háromszögbe írt $k_{0}$ kört metszi ki.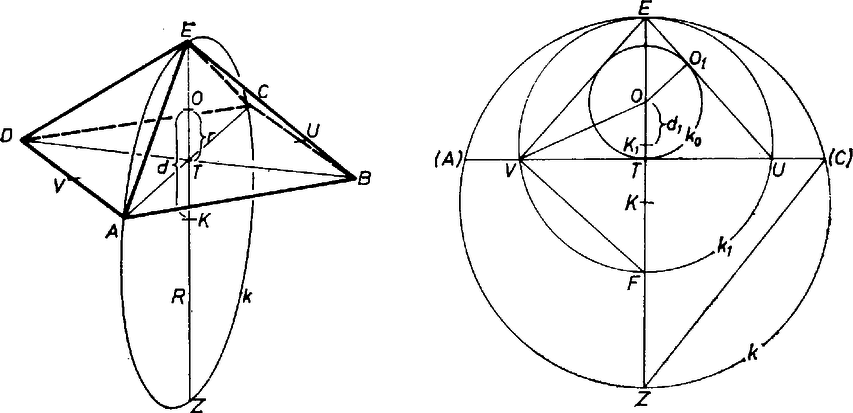

Jelöljük az

U V E

háromszög köré írt kört

k_{1}

-gyel, középpontját

K_{1}

-gyel, sugarát

R_{1}

-gyel, az

E

-vel átellenes pontját

F

-fel. Az

F O V

háromszögben

\begin{matrix} 2 F V O ∢ = U V E ∢ + U E V ∢, \\ 2 F O V ∢ = 180^{\circ} - U V E ∢ = V U E ∢ + U E V ∢, \end{matrix}

emiatt

O F = V F

. Jelöljük még

O

-nak

U E

-n levő vetületét

O_{1}

-gyel. Mivel az

E F V

E O O_{1}

háromszögek hasonlók,

\begin{matrix} V F : E F = O O_{1} : E O, \end{matrix}

vagyis

E O \cdot O F = E O \cdot V F = E F \cdot O O_{1} = 2 r R_{1}

. Jelöljük a

K_{1} O

szakasz hosszát

d_{1}

-gyel, akkor az

E O

O F

szakaszok közül az egyik hossza

(R_{1} + d_{1})

, a másiké

(R_{1} - d_{1})

, tehát

\begin{matrix} R_{1}^{2} - d_{1}^{2} = 2 r R_{1} . \end{matrix}

(2)

Ez Euler tétele, és ugyan a levezetésében részben kihasználtuk, hogy

U V E

egyenlő szárú, valójában erre nem volt szükségünk, mint ismeretes, meggondolásunk tetszőleges háromszögre kiterjeszthető.
Jelöljük

G

-nek az

A C E

síkkal alkotott metszés vonalát

k

-val,

k

-nak

E

-vel átellenes pontját

Z

-vel. Ekkor

\begin{matrix} E T \cdot T Z = T C^{2} = 2 T U^{2} = 2 E T \cdot T F, \end{matrix}

tehát

T Z = 2 T F

. Emiatt

\begin{matrix} 2 R_{1} = E F = 2 R - F Z = 2 R - T F = 2 R + r - O F, \end{matrix}

és így (2) alapján kapjuk, hogy

\begin{matrix} R^{2} - d^{2} = E O \cdot O Z = E O \cdot O F + E O \cdot O F - E O \cdot O T = \\ = r (2 R + r - O F) + 2 r R_{1} - r \cdot E O = r (2 R + r) + r (2 R_{1} - O F - E O) . \end{matrix}

Mivel

E O + O F = 2 R_{1}

, itt az utolsó tag 0, tehát épp azt kaptuk, amit bizonyítani akartunk.
A most bizonyított (1) összefüggés alapján ha

R = 1

, akkor

{(1 + r)}^{2} = 2 - d^{2}

, tehát

{(1 + r)}^{2}

maximuma 2,

r

maximuma

\sqrt[]{2} - 1

. Ez akkor érhető el, ha

d = 0

, vagyis

K

és

O

egybeesik. Ugyanazt kaptuk tehát, mint a F. 2096. megoldásában (KÖMAL 1978. január, 6‐7. oldal).