Kezdőlap


Feladat:	F.2124	Korcsoport: 16-17	Nehézségi fok: -
Füzet:	1978/április, 154 - 155. oldal		PDF \| MathML
Témakör(ök):	Koszinusztétel alkalmazása, Síkbeli szimmetrikus alakzatok, Sokszögek szimmetriái, Feladat
Hivatkozás(ok):	Feladatok: 1977/december: F.2124

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen egy nagy kör sugara $r$ . Nyilvánvaló, hogy a kis körök középpontjai közül 6 egy szabályos hatszög csúcsait adja, a hetedik pedig e hatszög középpontja. Az érintkezések és az egész ábra szimmetriái alapján a 6 nagy kör középpontjai is egy szabályos hatszög csúcsait adják és ezek az ábra $C$ centrumától $2 r$ távolságra vannak.
Tekintsük azt a háromszöget, amelyet a jobb felső nagy kör $O_{1}$ , a jobb oldali kis kör $O$ középpontja, valamint $C$ alkot, ebben $C O_{1} = 2 r$ , $C O = 2$ , $O_{1} O = r + 1$ és $O_{1} C O ∢ = 30^{\circ}$ , ennélfogva a cosinustétel alapján, majd 0-ra redukálva

\begin{matrix} {(r + 1)}^{2} = 4 r^{2} + 4 - 4 \sqrt[]{3} r, \\ r^{2} - \frac{2}{3} (1 + 2 \sqrt[]{3}) r + 1 = 0. \end{matrix}

Valóban másodfokú egyenletet kaptunk, anélkül, hogy erre törekedtünk volna. A leírt fölismerések alapján ugyanis csak így juthattunk közelebb

r

-hez. Most viszont ‐ mivel az egyenlet diszkriminánsa

16 (1 + \sqrt[]{3}) / 9 > 0

, így a gyökök valósak, másrészt mindkettő pozitív, hiszen összegük is, szorzatuk is pozitív‐, feladatunk előírása nélkül is meg kellene vizsgálnunk, melyik gyök felel meg, ha egyáltalán megfelel valamelyik.
Szövegünk, az

r > 1

"kiegészítő'' követelményt adja, de ezt nem használtuk fel a felállításban, nem is használhattuk volna! Az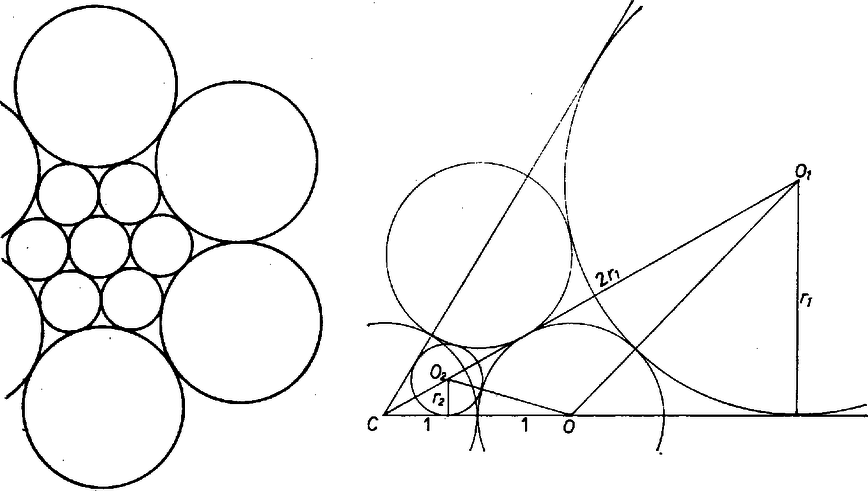

\begin{matrix} r_{1} = \frac{1}{3} (1 + 2 \sqrt[]{3} + 2 \sqrt[]{1 + \sqrt[]{3}}) = 2, 59 \end{matrix}

gyök ennek eleget tesz, és a mérés szerint a nagy és kis sugarak arányára ez megfelelő érték; elfogadjuk.

Egyenletünk együtthatóiból a két gyök szorzatára

r_{1} r_{2} = 1

, tehát

r_{1} > 1

alapján

0 < r_{2} = \frac{1}{r_{1}} < 1

. Ennek a következő jelentést tulajdoníthatjuk. Az

r_{1}

sugarú körök együttese, "koszorúja'' a

C

középpontú,

30^{\circ}

szögű,

\frac{1}{r_{1}}

arányszámú forgatva zsugorítással átmegy a kisebb körök koszorújába, ugyanez a transzformáció a kis koszorút egy még kisebb koszorúba viszi át, és

r_{2}

éppen ezt az új koszorút alkotó körök sugarát adja meg.
Valóban, visszatekintve az egyenlet felállítására, a következőket mondhatjuk. Azzal, hogy kis köreink sugarát ismertnek tekintjük, ezek mintegy kiindulási, "régi'' köröknek nevezhetők, és hozzájuk keressük a "másik méretű'', az "új'' körök sugarát. Egy "új'' kör
egyszerűsített leírása: a

C

centrumból félegyeneseket húzunk két szomszédos régi kör középpontján át, és az új körnek ezt a két félegyenest is és a vett két régi kört is érintenie kell (a szimmetria miatt ez nem 4 követelmény!). Ez "befelé'' éppúgy lehetséges, mint ahogyan kifelé. A felhasznált háromszög oldalai a "belső'' elképzelés szerint is 2,

2 r

és

(r + 1)

. Tehát "nagy'' helyett "új'' körökről beszélve,

r_{1}

és

r_{2}

egyenjogú megoldások.

Megjegyzések. 1. A megállapításból látható, hogy az eredeti ábra végtelen mintává fejleszthető tovább: tetszőleges kört felvéve, majd köré 6 ugyanekkora kört rajzolva, ezek köré újabb 6 egymást is érintő kör rajzolható stb.; illetve az eredeti középső kör helyett 6 még kisebb, egymást és a hat kis kört érintő kör rajzolható, ezekbe újabb 6 még kisebb kör stb. A minta mindig befejezhető úgy, hogy középre a 6 legkisebb körrel egyenlő nagyságú, ezeket érintő kört rajzolunk.
2. Tulajdonképpen önmagunknak nehezítjük meg a munkát, ha ilyen "előítéleteket'' viszünk be, mint "nagy'' kör. Az ábra zavarni is tud!