Kezdőlap


Feladat:	F.2118	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1978/március, 103 - 104. oldal		PDF \| MathML
Témakör(ök):	Húrnégyszögek, Síkgeometriai számítások trigonometria nélkül sokszögekben, Szabályos sokszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1977/november: F.2118

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Néhány próba alapján ezt sejtjük: olyan két átló összege egyenlő egy harmadikkal, amelyek közti szög $120^{\circ}$ . (ti. ha a két átlót a szabályos $3 k$ -szög egy csúcsából a két ellentétes körüljárási irányban választjuk meg, "lokalizáljuk''). Ezt fogjuk bizonyítani.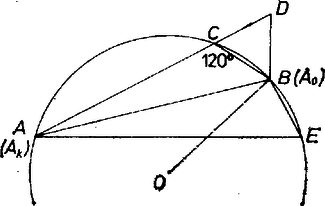

Legyen az

A B C

háromszögben a

C

-nél levő szög

120^{\circ}

, továbbá

C A ≧ C B

, az

A C

oldal

C

-n túli meghosszabbításán

D

az a pont, amelyre

C D = C B

, végül

D

tükörképe az

A B

egyenesre

E

. Ekkor a

B C D

háromszög egyenlő oldalú, ezért egyrészt

A E B ∢ = A D B ∢ = 60^{\circ} = 180^{\circ} - A C B ∢

; tehát az

E A C B

négyszög húrnégyszög,

E

rajta van az

A B C

háromszög körülírt körén, másrészt

A E = A D = A C + C B

.
Megmutatjuk, hogy a szabályos

3 k

-szög

A_{0}, A_{1}, A_{2}, ..., A_{k}, A_{k + 1}, ..., A_{3 k - 1}

csúcsai közül lehet kiválasztani olyan négyet, amelyeknek átadhatjuk az előbbi

A

C

B

és

E

pont szerepét. Nyilvánvalóan megfelel az

A = A_{k}

B = A_{0}

választás, mert így a rövidebbik

A B = A_{k} A_{0}

ívhez tartozó középponti szög

A_{0} O A_{k} ∢ = k \cdot \frac{360^{\circ}}{3 k} = 120^{\circ}

, a hosszabbik

A_{k} A_{0}

ívhez tartozó középponti szög

240^{\circ}

, így a rövidebb

A_{0} A_{k}

ív minden belső

C

pontjára

A_{0} C A_{k} ∢ = 120^{\circ}

. Itt

C

szerepére alkalmas minden olyan

A_{i}

csúcs, amely nem szomszédos sem

A_{0}

-lal, sem

A_{k}

-val, azaz amelyekre

A_{i} \neq A_{1}

és

A_{i} \neq A_{k - 1}

, vagyis amelyekre

2 ≦ i ≦ k - 2

. Ilyen sokszögcsúcs van, ha

k - 2 ≧ 2

, azaz

k ≦ 4

, továbbá ekkor

E

is sokszögcsúcs, hiszen

C

tükörképe a

B O

sugárra.
Feladatunk a

k > 4

reláció bizonyítása volt. A

k = 4

esetben két egyenlő hosszú átló összege egyenlő az

A_{0} A_{4}

átlóval. Az állítás

k > 4

-re tulajdonképpen ezt mondja: van kétféle olyan átlóhosszúság, amely ...; hiszen természetes, hogy szabályos sokszögben mindenféle átlóhosszúság annyi példányban van meg, mint az oldalak száma ‐ nyilvánvalóan kivéve a páros

2 m

oldalszámú sokszög leghosszabb átlóit, átmérőit:

A_{0} A_{m}, A_{1} A_{m + 1}, ..., A_{m - 1} A_{2 m - 1}

, amelyekből csak

m

példány van.

Megjegyzések. 1. A megfelelő átlópárokat csak egyszer kapjuk meg, ha

2 ≦ i ≦ \frac{k}{2}

, tehát számuk

[\frac{k}{2}] - 1

.
2. Lényegben ugyanez a bizonyítás, ha arra hivatkozunk, hogy a szabályos

A B F

háromszög köré írt kör bármely

P

pontjára a

P A

P B

P F

szakaszok közül a két kisebb együttvéve egyenlő a legnagyobbikkal.
3. Több dolgozat használta fel Ptolemaiosz (I.) tételét (konvex húrnégyszög átlóinak szorzata egyenlő a két-két szemben fekvő oldalból képezett szorzatok összegével).
4. Bizonyítható az állítás goniometriai úton is, annak fölhasználásával, hogy a szabályos

3 k

szög átlójára

\begin{matrix} A_{0} A_{i} = 2 r sin \frac{i}{2} \cdot \frac{360^{\circ}}{3 k} = 2 r sin \frac{i}{k} \cdot 60^{\circ}, (i = 1, 2, ..., 3 k - 1) . \end{matrix}