Kezdőlap


Feladat:	F.2115	Korcsoport: 16-17	Nehézségi fok: -
Megoldó(k):	Lengvárszky Zsolt , Németh Csóka Mihály
Füzet:	1978/március, 101. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Vektorok skaláris szorzata, Feladat
Hivatkozás(ok):	Feladatok: 1977/november: F.2115

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Vezessük be az $x = α + 60^{\circ}$ , $y = β + 60^{\circ}$ és $z = γ + 60^{\circ}$ jelöléseket. Mivel $α$ , $β$ és $γ$ egy háromszög szögei, $α + β + γ = 180^{\circ}$ , ezért $x + y + z = 360^{\circ}$ . A

\begin{matrix} cos z = cos [360^{\circ} - (x + y)] = cos (x + y) = cos x cos y - sin x sin y \end{matrix}

összefüggés alapján

(1)

a következő alakot ölti :

\begin{matrix} cos x + cos y + cos x cos y - sin x sin y + \frac{3}{2} ≧ 0. \end{matrix}

Az egyenlőtlenség mindkét oldalát

2

-vel megszorozva és

3

helyébe

(1 + {sin}^{2} x + {cos}^{2} x + {sin}^{2} y + {cos}^{2} y)

-t írva, a bizonyítandó egyenlőtlenségünk így alakul:

\begin{matrix} 1 + 2 cos x + 2 cos y + {cos}^{2} x + 2 cos x cos y + {cos}^{2} y + {sin}^{2} x - 2 sin x sin y + {sin}^{2} y = \\ {(1 + cos x + cos y)}^{2} + {(sin x - sin y)}^{2} ≧ 0. \end{matrix}

Lengvárszky Zsolt (Pécs, Komarov Gimn., III. o. t.)

II. megoldás.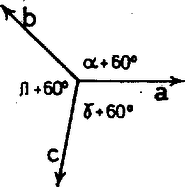

a

b

c

egységvektorokra legyen

\begin{matrix} (a, b) ∢ = α + 60^{\circ}, \\ (b, c) ∢ = β + 60^{\circ}, \\ (c, a) ∢ = γ + 60^{\circ} . \end{matrix}

Ez lehetséges, mivel

(α + 60^{\circ}) + (β + 60^{\circ}) + (γ + 60^{\circ}) = 360^{\circ}

(1. ábra). Vegyük az

a+b+c

vektor önmagával alkotott skaláris szorzatának felét. Erre nyilván

\begin{matrix} \frac{1}{2} {(a+b+c)}^{2} ≧ 0. \end{matrix}

Ha a négyzetre emelést elvégezzük, és figyelembe vesszük, hogy

a^{2} = b^{2} = c^{2} = 1

, valamint

ab = cos (α + 60^{\circ})

bc = cos (β + 60^{\circ})

és

ac = cos (γ + 60^{\circ})

, éppen a bizonyítani kívánt egyenlőtlenséget kapjuk.

Németh Csóka Mihály (Bp., Móricz Zs. Gimn., IV. o. t.)

Megjegyzés. Egyenlőség csak akkor következik be, ha

a +b +c = 0

, ami viszont csak akkor teljesül, ha

α = β = γ = 60^{\circ}