Kezdőlap


Feladat:	F.2109	Korcsoport: 14-15	Nehézségi fok: könnyű
Megoldó(k):	Ármós Lajos , Piros Sándor , Spilkó József
Füzet:	1978/február, 61 - 62. oldal		PDF \| MathML
Témakör(ök):	Szélsőérték differenciálszámítással, Két pont távolsága, szakasz hosszúsága, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1977/október: F.2109

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a vizsgált kifejezést $f (x)$ -szel. Az $f (x)$ minden valós $x$ számra értelmezve van, hiszen a gyökjelek alatt különböző számok négyzetösszege szerepel, ami mindig pozitív. Így $f (x)$ értéke is mindig pozitív. Nem negatív számok körében a négyzetre emelés monoton művelet, ezért $f^{2} (x)$ ugyanott minimális, ahol $f (x)$ .

\begin{matrix} f^{2} (x) = {(\sqrt[]{2 x^{2} + 1 + 2 x} + \sqrt[]{2 x^{2} + 1 - 2 x})}^{2} = 4 x^{2} + 2 + 2 \sqrt[]{4 x^{4} + 1} . \end{matrix}

Erről a kifejezésről közvetlenül megállapítható, hogy legkisebb értékét

x = 0

-nál veszi fel.

Piros Sándor (Debrecen, Fazekas M. Gimn., III. o. t.)

II. megoldás. Tekintsük azt a háromszöget, amelynek csúcsai a síkbeli

(x, y)

derékszögű koordináta-rendszerben

A (0; - 1)

B (x; x)

C (0; 1)

(l. ábra). A háromszög egyenlőtlenség alapján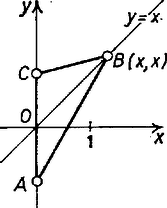

\begin{matrix} A C \leq A B + B C . \end{matrix}

Az egyenlőtlenségben szereplő távolságokat a koordinátákkal kifejezve

\begin{matrix} 2 \leq \sqrt[]{x^{2} + {(x + 1)}^{2}} + \sqrt[]{x^{2} + {(x - 1)}^{2}} \end{matrix}

adódik. Egyenlőség akkor és csak akkor áll fenn, ha az

A B C

háromszög elfajuló, és

B

A C

oldalszakasz pontja.

x

változik,

B

y = x

egyenes mentén mozog. Az egyenlőség tehát akkor és csak akkor következik be, ha

B

az origóban van, vagyis

x = 0

. Mivel az egyenlőtlenség jobb oldalán éppen a vizsgált kifejezés szerepel, ezzel a feladat kérdésére meg is adtuk a választ.
Az egyenlőtlenség bal oldalán a minimum értéke is ‐ mintegy magától ‐ előbukkant.

Ármós Lajos (Debrecen, Fazekas M. Gimn., IV. o. t.)

Megjegyzés. A közölt megoldás alapján a feladat könnyen általánosítható.

III. megoldás (vázlat). A feladatot a differenciálszámítás felhasználásával oldjuk meg. Az

f (x) = \sqrt[]{x^{2} + {(x + 1)}^{2}} + \sqrt[]{x^{2} + {(x - 1)}^{2}}

minden valós

x

számra értelmezett folytonos és differenciálható függvény, deriváltja

\begin{matrix} f' (x) = \frac{2 x + 1}{\sqrt[]{2 x^{2} + 2 x + 1}} + \frac{2 x - 1}{\sqrt[]{2 x^{2} - 2 x + 1}} . \end{matrix}

Ez szintén mindenütt értelmezett és folytonos függvény.
Az

f' (x) = 0

egyenletet megoldva egyetlen gyök,

x = 0

adódik. Mivel a derivált függvény folytonos, a

(- \infty; 0)

és a

(0; \infty)

intervallumban állandó előjelű;

f' (- 1) = - 1 - \frac{3}{\sqrt[]{5}} < 0

és

f' (1) = \frac{3}{\sqrt[]{5}} > 0

alapján

(- \infty; 0)

-ban negatív,

(0; \infty)

-ben pozitív. Ezek szerint

f (x)

(- \infty; 0)

-ban fogyó, a

(0; \infty)

-ben növekedő. Így

f (x)

-nek

x = 0

-nál abszolút minimuma van.

Spilkó József (Tatabánya, Árpád Gimn., IV. o. t.)