Kezdőlap


Feladat:	F.2108	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1978/január, 13 - 14. oldal		PDF \| MathML
Témakör(ök):	Vetítések, Derékszögű háromszögek geometriája, Térgeometriai bizonyítások, Feladat
Hivatkozás(ok):	Feladatok: 1977/szeptember: F.2108

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Pitagorasz tételét felírva az $A E P$ , $B F P$ , $C G P$ , $D H P$ , valamint $E B P$ , $F C P$ , $G D P$ , $H A P$ derékszögű háromszögekre (1. ábra), fejezzük ki az állítás bal és jobb oldalán álló összeadandókat:

\begin{matrix} A E^{2} = A P^{2} - P E^{2}, E B^{2} = B P^{2} - P E^{2}, \\ B F^{2} = B P^{2} - P F^{2}, F C^{2} = C P^{2} - P F^{2}, \\ C G^{2} = C P^{2} - P G^{2}, G D^{2} = D P^{2} - P G^{2}, \\ D H^{2} = D P^{2} - P H^{2}, H A^{2} = A P^{2} - P H^{2} . \end{matrix}

A bal és a jobb oldalon álló tagok helyébe a fenti különbségeket írva látható, hogy valóban fennáll az egyenlőség.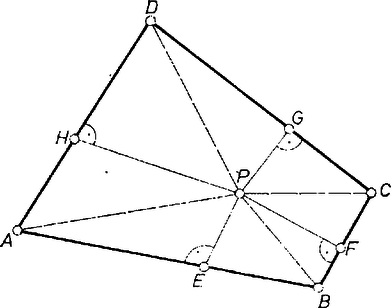

1. ábra

Vizsgáljuk most a feladat második részét! Megmutatjuk, hogy a szereplő feltételek mellett igaz az első részben bizonyított tétel megfordítása, azaz ha teljesül (1), akkor a kérdéses síkok egy ponton mennek át.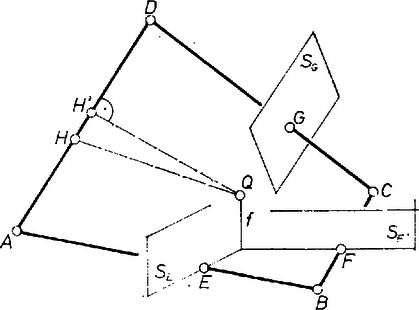

2. ábra

E

-n átmenő,

A B

egyenesre merőleges és az

F

-en átmenő,

B C

egyenesre merőleges síkok különbözők és nem párhuzamosak, mivel az

A

B

C

pontok nincsenek egy egyenesen (különben ugyanis

A

B

C

D

egy síkban lennének). E két sík tehát metszi egymást, legyen metszésvonaluk

f

(2. ábra). Hasonlóan a

G

-n átmenő,

D C

egyenesre merőleges sík nem tartalmazza

f

-et és nem párhuzamos

f

-fel,

f

tehát döfi ezt a síkot, legyen a döféspont

Q

. Ekkor

Q

vetülete az

A B

B C

C D

egyenesen rendre

E

F

G

. Legyen a

Q

pontnak az

A D

egyenesen levő vetülete

H'

. Ekkor az első rész állítása szerint

\begin{matrix} A E^{2} + B F^{2} + C G^{2} + D H'^{2} = E B^{2} + F C^{2} + G D^{2} + H' A^{2} . \end{matrix}

(2)

(1) és (2) különbségét képezve rendezés után kapjuk, hogy

\begin{matrix} D H^{2} - H A^{2} - D H'^{2} - H' A^{2} . \end{matrix}

(3)

A távolságokat előjeles távolságoknak tekintve, és felhasználva, hogy

D H + H A = D H' + H' A = D A

, kapjuk, hogy

D H' = D H

, azaz

H' = H

.
Tehát a

H

-n átmenő és az

A D

egyenesre merőleges sík is átmegy a

Q

ponton, vagyis a négy vizsgált sík egy ponton megy át.