Kezdőlap


Feladat:	F.2107	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1978/január, 11 - 12. oldal		PDF \| MathML
Témakör(ök):	Középpontos és egyéb hasonlósági transzformációk, Súlyvonal, Kör egyenlete, Ellipszis egyenlete, Kör (és részhalmaza), mint mértani hely, Párhuzamos szelők tétele, Háromszögek szerkesztése, Ellipszis, mint mértani hely, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1977/szeptember: F.2107

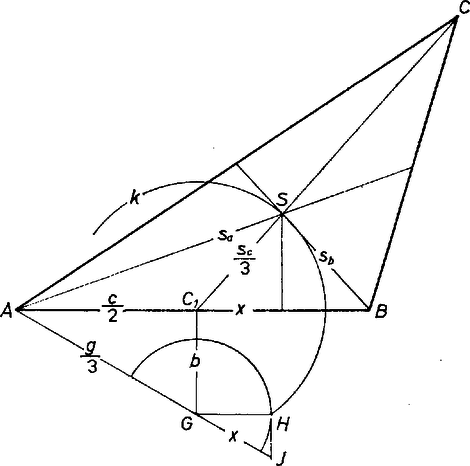
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a keresett $A B C$ háromszögben az adott $A B$ oldal hosszát $c$ -vel, felezőpontját $C_{1}$ -gyel, az adott $C C_{1}$ súlyvonal hosszát $s_{c}$ -vel, a további két $s_{a}$ és $s_{b}$ súlyvonal összegét $g$ -vel, a súlypontot $S$ -sel. A súlypont ismert harmadoló tulajdonsága alapján elegendő az $A B = c$ alaphoz úgy meghatározni $S$ -et, hogy $S C_{1} = \frac{s_{c}}{3}$ és $S A + S B = \frac{2 g}{3}$ legyen, ezután $C$ az $S$ -nek $3$ -szorosra nagyított képe a $C_{1}$ -ből mint centrumból. Ezzel két mértani helyet kaptunk $S$ -re: a $C_{1}$ körüli $\frac{s_{c}}{3}$ sugarú $k$ kört és azt az $e$ ellipszist, amelynek fókuszai $A$ és $B$ , nagytengelyének hossza $\frac{2 g}{3}$ .
A $k$ és $e$ mértani helyek centruma közös, mindkettő tükrös az $A B$ egyenesre és az $A B$ szakasz felező merőlegesére, tehát bármelyik két közös pontjuk tükrözéssel egymásba átvihető. Ezért a feladatnak lényegében 1 megoldása van, ha létezik közös pont, különben nincs megoldása.
Közös pont létezéséhez nyilvánvalóan szükséges a következő két föltétel teljesülése, és egyben elegendő is: $A S + B S > A B$ azaz $\frac{2 g}{3} - c > 0$ ; a kör átmérője essék $e$ -nek kis‐ és nagytengelye közé:

\begin{matrix} \sqrt[]{\frac{4 g^{2}}{9} - c^{2}} \leq \frac{2 s_{c}}{3} < \frac{2 g}{3}, \end{matrix}

az átmérő a kistengellyel egyenlő is lehet ‐ ekkor egyenlő szárú háromszöget ad a közös

S

pont ‐, de a nagytengellyel nem, mert úgy a közös pont az

A B

egyenesre esnék.
Ez az elvi megoldás azonban nem követhető eukleidészi szerkesztéssel, mert

e

-ből csak véges számú pontot tűzhetünk ki. Emiatt számítással készítjük elő a szerkesztést.
Egyszerűsitésül előbb az

x^{2} + y^{2} = r^{2}

egyenletű körrel és az

\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1

(a > b > 0)

egyenletű ellipszissel foglalkozunk. Közös pontjuk koordinátái abszolút értékben:

\begin{matrix} x = a \sqrt[]{\frac{r^{2} - b^{2}}{a^{2} - b^{2}}}, y = b \sqrt[]{\frac{a^{2} - r^{2}}{a^{2} - b^{2}}} . \end{matrix}

(Az ordinátát csak avégett írtuk fel, hogy

y \neq 0

esetére lássuk a fentire vezető

b \leq r < a

föltételt.)
Esetünkben

\begin{matrix} a = \frac{g}{3}, b^{2} = {(\frac{g}{3})}^{2} - {(\frac{c}{2})}^{2}, a^{2} - b^{2} = {(\frac{c}{2})}^{2}, r^{2} = \frac{s_{c}^{2}}{9}, \end{matrix}

és így

\begin{matrix} x \sqrt[]{r^{2} - b^{2}} = \frac{g}{3} : \frac{c}{2}, \end{matrix}

ezek alapján szerkesztésünk a következő:

A B = c

szakasz felező merőlegesét metsszük az

A

körüli,

\frac{g}{3}

sugarú körrel a

G

pontban, így

C_{1} G = b

; a

G

-n átmenő,

A B

-vel párhuzamos egyenesből a

k

körrel kimetsszük azt a

H

pontot, amelyre

H B < H A

, így

G H = \sqrt[]{r^{2} - b^{2}}

; az

A G

egyenest metsszük a

H

-n átmenő,

A B

-re merőleges egyenessel

J

-ben, ekkor a párhuzamos szelők tétele alapján

G J = x

. Ezután

x

-et felmérjük a

C_{1} B

szakaszra, a végpontjában

A B

-re állított merőleges

k

-ből kimetszi

S

-et. Innen már láttuk a befejezést.
II. megoldás. Kiszámítjuk az

S A = \frac{2}{3} s_{a}

szakaszt (és vele tulajdonképpen

S B = \frac{2}{3} s_{b}

-t is, mondhatjuk így is: a fönti ellipszisben az

S

pont vezérsugarait) a súlyvonalaknak a háromszög

a

b

c

oldalaival való ismert összefüggései ^{$^{*}$} alapján. Látni fogjuk, hogy a nagyobbik vezérsugár egyenlő a föntiek szerint már rendelkezésünkre álló

A G

és

G H

szakaszok összegével (a kisebbik pedig ezek különbsége). Ekkor

S

-et a fönti

k

körből az

A

körüli

S A

sugarú körrel metszhetjük ki.

s_{a}

és

s_{b}

a következő másodfokú egyenlet gyökei:

\begin{matrix} u^{2} - (s_{a} + s_{b}) u + s_{a} s_{b} = u^{2} - g u + s_{a} s_{b} = 0. \\ 2 u_{12} = g \pm \sqrt[]{g^{2} - 4 s_{a} s_{b}} . \end{matrix}

Ezekhez

\begin{matrix} s_{a}^{2} = \frac{1}{4} (2 b^{2} + 2 c^{2} - a^{2}), s_{b}^{2} = \frac{1}{4} (2 a^{2} + 2 c^{2} - b^{2}), s_{c}^{2} = \frac{1}{4} (2 a^{2} + 2 b^{2} - c^{2}); \end{matrix}

tehát

\begin{matrix} 2 s_{a} s_{b} = {(s_{a} + s_{b})}^{2} - (s_{a}^{2} + s_{b}^{2}) = g^{2} - \frac{1}{4} (4 c^{2} + a^{2} + b^{2}) = g^{2} - c^{2} - \frac{1}{4} \cdot \frac{4 s_{c}^{2} + c^{2}}{2}, \\ g^{2} - 4 s_{a} s_{b} = - g^{2} + \frac{9}{4} c^{2} + s_{c}^{2} = 9 {{(\frac{s_{c}}{3})}^{2} - [{(\frac{g}{3})}^{2} - {(\frac{c}{2})}^{2}]}, \end{matrix}

így a két vezérsugár nagyobbika valóban

\begin{matrix} \frac{2}{3} s_{a} = \frac{g}{3} + \sqrt[]{{(\frac{s_{c}}{3})}^{2} - [{(\frac{g}{3})}^{2} - {(\frac{c}{2})}^{2}]} = \\ = A G + \sqrt[]{C_{1} H^{2} - (A G^{2} - A C_{1}^{2})} = A G + \sqrt[]{C_{1} H^{2} - C_{1} G^{2}} = A G + G H, \end{matrix}

amint állítottuk.

^{$^{*}$}Ha

C

tükörképe

C_{1}

-re

C^{*}

, akkor a

C A C^{*} B

paralelogrammában az átlók négyzetösszege egyenlő az oldalak négyzetösszegével.