Kezdőlap


Feladat:	F.2101	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Baksai R. , Balázs I. J. , Benkő T. , Bessenyei B. , Bukta Gy. , Csapó Ildikó , Cseke I. , Csikós B. , Fegyverneki S. , Fordán T. , Geiger Ilona , Horváth L. , Hülber E. , Ivanyos G. , Knébel I. , Koncz K. , Nagy G. , Pósafalvi A. , Rapai T. , Spissich L. , Tábori L. , Tóth Cs. , Vágvölgyi S. , Varga G. , Zempléni A.
Füzet:	1977/november, 135 - 136. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Egyenlő szárú háromszögek geometriája, Diszkusszió, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1977/május: F.2101

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az alap végpontjait $B$ -vel, $C$ -vel, a szemközti csúcsot $A$ -val, a $C$ -ből induló szögfelező $A B$ -n levő pontját $F$ -fel, és mérjük fel $B C$ -nek $B$ -n túli meghosszabbítására a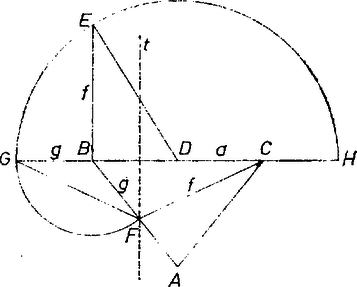

\begin{matrix} B G = B F = g \end{matrix}

szakaszt.

A kapott

B F G

háromszög egyenlő szárú, és az alapján levő szögei az

A B C

háromszög

B

-nél levő szögének a felével egyenlőek. Emiatt

C F G

is egyenlő szárú, és hasonló

G F B

-hez. Így

B G : G F = F C : C G

, vagyis

\begin{matrix} g : f = f : (g + a) . \end{matrix}

(1)

g

-re másodfokú egyenlet, amelynek gyökei

\begin{matrix} g_{12} = - \frac{a}{2} \pm \sqrt[]{{(\frac{a}{2})}^{2} + f^{2}}, \end{matrix}

tehát (1)-nek mindig pontosan egy pozitív gyöke van:

\begin{matrix} g = \sqrt[]{{(\frac{a}{2})}^{2} + f^{2}} - \frac{a}{2} . \end{matrix}

(2)

Mérjük fel a

B C = a

szakaszra merőlegesen a

B E = f

szakaszt, és rajzoljunk

B C

-nek

D

felezőpontja körül

E

-n átmenő kört. Messe ez

B C

-t a

G

H

pontokban

(G B < H B)

, akkor a kör húrjaira vonatkozó tétel szerint

B E^{2} = B G \cdot B H

, tehát a

B G = C H = g

szakasz az (1) egyenlet pozitív gyöke. Rajzoljunk

B

körül

G

-n átmenő kört, messe ez

C G

-nek

t

felező merőlegesét

F

-ben. Megmutatjuk, hogy ha

F

létrejön és

B E

-nek

C

-t tartalmazó oldalán van, akkor ez az, amit kerestünk, tehát belőle a

B C F

szöget megduplázva a keresett

A B C

háromszöget kapjuk. Ha pedig a feltételeink nem teljesülnek, akkor nincs a feladatnak megoldása.
A most megszerkesztett

F

pont mellett

B F G

és

F C G

hasonló egyenlő szárú háromszögek, tehát a

C F = G F = x

szakaszra

\begin{matrix} g : x = x : (g + a) \end{matrix}

teljesül, így az (1) alapján egyenlő

f

-fel. Mivel a

C B F ∢

kétszerese a

B C F = B G F

szögnek, a

B C F

szög megduplázásával valóban a keresett háromszöget kapjuk, ha a

B C F

szög hegyesszög. Ennek és

F

létrejöttének a feltétele

\begin{matrix} g > \frac{a + g}{2} - g > 0, \end{matrix}

ami (2) szerint ekvivalens azzal, hogy

\begin{matrix} \frac{2}{3} a < f < \sqrt[]{2} a . \end{matrix}

(3)

Ez tehát a szerkeszthetőség feltétele, és nyilván ez a megoldás létezésének is a feltétele.
A mondott

f = a

és

f = a / \sqrt[]{2}

speciális esetekre teljesül (3), így a szerkesztés végrehajtható. Az első esetben

B E = B C

, tehát

E

és

C

annak az

a

sugarú körnek a pontjai, amelybe írt szabályos tízszögnek egyik cikke a

B C F

háromszög. Ráismerhetünk a

B F = g

szakasz klasszikus szerkesztésére a fenti megoldásban, mi mintegy azt általánosítottuk az

f \neq a

esetre.
Ha pedig

f = a / \sqrt[]{2}

, akkor (2) szerint

\begin{matrix} a - g = (3 - \sqrt[]{3}) \frac{a}{2} = \sqrt[]{3} g, \end{matrix}

tehát

D B F ∢ = 30^{\circ}

Megjegyzés. A

C G F

háromszög alapján levő

δ

szögre

\begin{matrix} cos δ = \frac{C G}{2 G F} = \frac{a + g}{2 f}, \end{matrix}

így a

cos δ

ismeretlenre ugyanúgy másodfokú egyenletet kapunk, mint

g

-re. A megoldók többsége ezt az utat választotta.