Feladat:	F.2096	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Csapó Ildikó ,  Horváth László ,  Molnár Éva
Füzet:	1978/január, 6 - 7. oldal		PDF  |  MathML
Témakör(ök):	Beírt gömb, Szélsőérték differenciálszámítással, Szabályos sokszög alapú gúlák, Négyszög alapú gúlák, Körülírt kör, Beírt kör, Feladat
Hivatkozás(ok):	Feladatok: 1977/április: F.2096

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.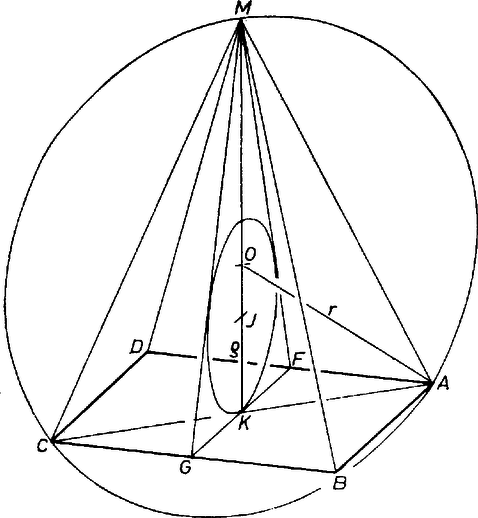   Legyen a gúla alaplapja az $ABCD$ négyzet, az ezzel szemben fekvő (fő) csúcsa $M$, az $AD$ és $BC$ él felezőpontja $F$, ill. $G$ és $FG$ felezőpontja $K$. Ekkor a körülírt gömb középpontja azonos az $MAC$ átlós síkmetszet köré írt kör $O$ középpontjával és sugara $r=OA$; másrészt hasonlóan ‐ csupán más megfogalmazással ‐ a beírt gömbből az $MFG$ sík által kimetszett főkör az $MFG$ háromszög beírt köre. Ennek középpontját $J$-vel jelölve a sugár $\varrho =JK$. Legyen még $AB=1$, ekkor feladatunk a $KM=x$ magasságra annak az értéknek meghatározása, amelyre az $y=\frac{OA}{JK}$ hányados a legkisebb. Mármost ismert összefüggések alapján, majd deriválással ${\displaystyle \begin{array}{c}\hfill {\displaystyle r\left(=\frac{abc}{4t}\right)=\frac{\sqrt[]{2}\cdot M{A}^2}{2AC\cdot KM}=\frac{2x^2+1}{4x}\mathrm{,}}\hfill \\ \hfill {\displaystyle \varrho \left(=\frac{2t}{2s}\right)=\frac{FG\cdot KM}{1+2FM}=\frac{x}{1+\sqrt[]{4x^2+1}}\mathrm{,}}\hfill \\ \hfill {\displaystyle y=\frac{r}{\varrho }=\frac{2x^2+1}{4x^2}\left(1+\sqrt[]{4x^2+1}\right)=\left(\frac{1}{2}+\frac{1}{4x^2}\right)\left(1+\sqrt[]{4x^2+1}\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle y\text{'}=-\frac{1}{2x^3}\left(1+\sqrt[]{4x^2+1}\right)+\left(\frac{1}{2}+\frac{1}{4x^2}\right)\frac{4x}{\sqrt[]{4x^2+1}}=}\hfill \\ \hfill {\displaystyle =\frac{4x^4-2x^2-1-\sqrt[]{4x^2+1}}{2x^3\sqrt[]{4x^2+1}}\mathrm{.}}\hfill \end{array}}$ A számláló $0$, ha $\begin{array}{c}{\displaystyle 4x^4-2x^2-1=\sqrt[]{4x^2+1}\mathrm{,}}\end{array}$ amiből négyzetre emeléssel, majd mivel minket csak a valós, pozitív zérushely érdekel $\begin{array}{c}{\displaystyle 4x^4\left(4x^4-4x^2-1\right)=\mathrm{0,}{x}_0=\sqrt[]{\frac{1+\sqrt[]{2}}{2}}\left(=1\mathrm{,}099\right)\mathrm{.}}\end{array}$ Csak az $x_0$ helyen lehet szélső értéke a hányadosnak, ekkor $\begin{array}{c}{\displaystyle \sqrt[]{4x_0^2+1}=1+\sqrt[]{2}\text{és}{y}_0=1+\sqrt[]{2}\left(=2\mathrm{,}414\right)\mathrm{.}}\end{array}$ Tekintsük függvényünk értékét az $x=1$ $\left(<x_0\right)$ és az $x=\sqrt[]{2}\left(>x_0\right)$ helyeken: $\begin{array}{c}{\displaystyle \frac{3\left(1+\sqrt[]{5}\right)}{4}\left(=2\mathrm{,}427\right)\mathrm{,}\text{ill.}\frac{5}{2}\left(=2\mathrm{,}5\right)\mathrm{,}}\end{array}$ mindkettő nagyobb, mint $y_0$, tehát $x_0$-ban az $\frac{r}{\varrho }$ hányadosnak minimuma van. $x_0$-ból a gúla minden egyéb mérete kiszámítható.    Horváth László (Csurgó, Csokonai Vitéz M. Gimn., IV. o. t.)   Megjegyzés. Az $x_0$ magasság mellett $r=\frac{1}{2}\sqrt[]{\sqrt[]{2}+1}$, $\varrho =\frac{1}{2}\sqrt[]{\sqrt[]{2}-1}$, ezekből $r^2-\frac{1}{2}={\varrho }^2$, $O{A}^2-K{A}^2=J{K}^2$, tehát a körülírt és a beírt gömb középpontja ekkor egybeesik.