Kezdőlap


Feladat:	F.2089	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Baksai R. , Balázs I. J. , Baranyai Á. , Blázsik Z. , Boros L. , Cseke I. , Erdélyi T. , Knébel I. , Koncz K. , Lenkei P. , Nagy I. (Debrecen) , Németh R. (Győr) , Pusztai V. , Samu Viktória , Spilkó J. , Székely Z. , Szőke R. , Tóth Cs. , Ujj L. , Zempléni A.
Füzet:	1977/november, 131. oldal		PDF \| MathML
Témakör(ök):	Egyenlő szárú háromszögek geometriája, Szögfelező egyenes, Beírt kör középpontja, Diszkusszió, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1977/március: F.2089

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $O C_{1} B$ háromszög egyenlő szárú, ugyanis $C_{1} O B ∢ = O B C ∢$ , mert váltószögek, és $C_{1} O B ∢ = O B C ∢$ , mert $O B$ a $C B A ∢$ szögfelezője. Így 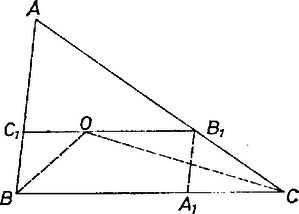$O C_{1} = C_{1} B$ .

Ugyanígy

C B_{1} = O B_{1}

tehát a

B C B_{1} C_{1}

trapéznek mind a négy oldalát ismerjük. Nyilvánvalóan szükséges feltétele a háromszög létezésének, hogy teljesüljön

\begin{matrix} B C > O C_{1} + O B_{1} . \end{matrix}

(1)

A trapéz szerkesztése visszavezethető az

A_{1} B_{1} C

háromszög szerkesztésére, ahol

A_{1} B_{1} ∥ A B

és

A_{1}

rajta van

B C

-n, a szerkesztés menete:
Megszerkesztjük az említett háromszöget az

A_{1} B_{1} = O C_{1}

B_{1} C = O B_{1}

és

A_{1} C = B C - (O B_{1} + O C_{1})

szakaszokból. Eltoljuk

A_{1} B_{1}

-t

\vec{C A_{1}}

irányú,

O B_{1} + O C_{1}

nagyságú vektorral, így a

B C B_{1} C_{1}

trapézt kapjuk, végül a

B_{1} C

és

B C_{1}

egyenesek metszéspontja

A

.
A szerkesztés pontosan akkor végezhető el, ha az

A_{1} B_{1} C

háromszög szerkeszthető. Ennek szükséges és elégséges feltétele, hogy e háromszög oldalaira fennálljon a háromszög-egyenlőtlenség:

\begin{matrix} B C - (B_{1} O + O C_{1}) < O B_{1} + O C_{1}, \\ O B_{1} < B C - (O B_{1} + O C_{1}) + O C_{1} és \\ O C_{1} < B C - (O B_{1} + O C_{1}) + O B_{1}, \end{matrix}

azaz

\begin{matrix} B C < 2 (O B_{1} + O C_{1}), & (2) \\ 2 \cdot O C_{1} < B C, & (3) \\ 2 \cdot O B_{1} < B C . & (4) \end{matrix}

Észrevehetjük, hogy az (1) feltétel (3) és (4) következménye, így a (2), (3) és (4) teljesülése a szerkeszthetőség feltétele. Ekkor a szerkesztés menetéből látszik, hogy az

A B C

háromszög egybevágóság erejéig meghatározott.
Meg kell még mutatnunk, hogy a szerkesztés helyes, a kapott

A B C

háromszög beírt körének középpontja a rajta átmenő

C_{1} B_{1}

szakaszt valóban az adott hosszúságú

O C_{1}

O B_{1}

szakaszokra osztja. Ehhez elegendő belátni, hogy

O

rajta van a

B

és

C

csúcsokból induló szögfelezőn. A szerkesztés miatt az

O C_{1} B

háromszög egyenlő szárú, így

C_{1} O B ∢ = O B C_{1} ∢

. Mivel

C B ∥ C_{1} B_{1}

a szerkesztés miatt, így

C_{1} O B ∢ = O B C ∢

, azaz

O B C ∢ = O B C_{1} ∢

, tehát

O

rajta van a

B

szög szögfelezőjén. Ugyanígy látható be, hogy

O

rajta van a

C

szög szögfelezőjén.