Feladat: F.2084 Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Balázs I. J. ,  Csapó Ildikó ,  Cseke I. ,  Csikós B. ,  Erdélyi T. ,  Fegyverneki S. ,  Filakovszky P. ,  G. Horváth Á. ,  Hülber E. ,  Ivanyos G. ,  Knébel I. ,  Koncz K. ,  Kozma J. ,  Lukács 258 Erzsébet ,  Németh 892 R. ,  Pyber L. ,  Rapai T. ,  Sali A. ,  Szabó 325 A. ,  Székely Z. ,  Szőke R. ,  Tóth Cs. 
Füzet: 1977/november, 127 - 128. oldal  PDF  |  MathML 
Témakör(ök): Beírt gömb, Vetítések, Hozzáírt körök, Súlypont, Alakzatok súlypontja (tömegközéppontja), Tetraéderek, Feladat
Hivatkozás(ok):Feladatok: 1977/február: F.2084

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A homogén anyagú BCD háromszöglap geometriai értelemben vett SA súlypontja egyúttal dinamikai értelemben a rá ható elemi súlyerők eredőjének támadópontja. Ennélfogva e lap mA=k1tA tömegét SA-ba sűrítve gondolhatjuk, itt tA a lap területét, a k1 arányossági tényező pedig az anyag ,,felületi sűrűségét'' jelenti. Ezt folytatva, elég meghatároznunk a négy SX pontból álló, tX tömeget tartalmazó pontrendszer súlypontját ‐ ahol rendre X=A, B, C, D ‐, hiszen k1-et további közlés hiányában nyilván csak mind a négy lapra vonatkozóan ugyanakkorának vehetjük.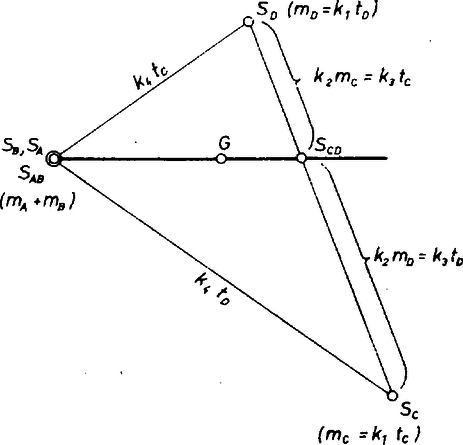

 

 

Tovább 2-2 pontunk tömegét vonjuk össze. Az SX- és SY-beli tömegekből álló pár (Y≠X) közös súlypontja az SXSY szakasznak abban az SXY pontjában van, amelyre (a nyomatékok egyezése alapján) SXYSX:SXYSY=mY:mX=tY:tX, másképpen, alkalmas k2 és k3 arányossági tényezővel SXYSX=k2mY-k3tY. Ugyanezzel az elvvel kapjuk a kérdéses G súlypontot, egyik tömegpárban X-et és Y-t A-nak, B-nek választva, az SABSCD szakaszon.
Felhasználjuk továbbá, hogy mind a négy XSX szakasz átmegy az ABCD tetraéder S súlypontján úgy, hogy SX=3⋅SSX, tehát az SASBSCSD tetraéder az előbbiből centrális hasonlósággal áll elő. (Az arányszám értéke -1/3, de ez nem lesz lényeges.) Ebből következik, hogy az új tetraéder bármelyik két lapja területének az aránya megegyezik a megfelelő eredeti lapok t-arányával, pl. (röviden, jelképesen):
(SASBSC):(SASBSD)=(ABC):(ABD)=tD:tC.

Vetítsük most az új tetraédert egy, az SASB élére merőleges síkra ‐ más szóval: nézzünk rá végtelen távolból, ebből az irányból ‐, és jelöljük a vetületeket ‐ mint látszó képeket ‐ ugyanúgy, mint magukat a pontokat. Csak az SASCSD háromszöget látjuk, tekintsük ebben az SA-ból induló két oldal arányát. Az SASC és SASD hosszakban az SASBSC, ill. SASBSD háromszögnek azt a magasságát látjuk valódi nagyságban, amelyik merőleges a közös SASB oldalukra. Ennélfogva arányuk egyezik e két háromszög területének arányával, az pedig az előbbi példa szerint tD:tC, végül is SASC=k4tD, SASD=k4tC, ahol k4 alkalmas arányossági tényező.
Most már az SCDSC:SCDSD=SASC:SASD aránypárból következik, hogy SCD rajta van a látszó háromszög SA-ból induló szögfelezőjén, és hogy ezen a felezőn látjuk a keresett G-t is. Ámde egyeneseink az ábra síkjára merőleges síkoknak a képei, tehát G rajta van az újabb tetraéder SASBSC és SASBSD lapjai közti lapszöget felező síkon; így pedig G-nek e két lapsíktól mért távolsága egyenlő; célszerű jelöléssel rD=rC.
Alkalmazzuk eredményünket úgy, hogy az SX pontok első párja A és C, majd pedig úgy, hogy B és C legyen, így rD=rB, majd rA=rD, tehát G az SX tetraédernek mind a négy lapjától egyenlő távolságra van. Ezzel bebizonyítottuk a feladat állítását.
 
Megjegyzések. 1. A bebizonyított állítás a lapsúlypontok igénybevétele nélkül ezt is jelenti: ha a tetraéder mindegyik csúcsába a szemben levő lap területével arányos tömeget teszünk, a pontrendszer súlypontja megadja a tetraéderbe beírható gömb középpontját.
2. Mind a háromszögre, mind a gömbre vonatkozóan hasonló súlypont-értelmezést kapunk a háromszöghöz hozzáírt körök (külső érintő körök) középpontjára, ill. a hozzáírt gömbök középpontjára ‐ amennyiben a háromszög valamelyik oldalának negatív súlyt tulajdonítunk (vonzóerő helyett ellentétes irányú, felfelé ható erőt). Tetraéder esetében összesen 8 érintő gömb lehetséges, mert egyszerre 2 lapnak is adhatunk negatív súlyt, de pl. szabályos tetraéder esetében csak 5 jön létre.
3. A bizonyítások természetesen vektorok felhasználásával is végezhetők.