2CMF2078 feladat dekódolása nem sikerült.
Feladat: 2CMF2078 Korcsoport: 18- Nehézségi fok: átlagos
Megoldó(k):  Horváth László ,  Kovács Zsolt 
Füzet: 1977/szeptember, 13 - 14. oldal  PDF  |  MathML 
Témakör(ök): Vetítések, Kocka, Terület, felszín, Szélsőérték-feladatok differenciálszámítás nélkül, Térgeometria alapjai, Feladat
Hivatkozás(ok):Feladatok: 2CMF2078 feladat dekódolása nem sikerült.
1977/január: 2CMF2078

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a kocka alaplapja ABCD, fedőlapja EFHG. Ha a kockát egy, a PQ egyenesre merőleges S0 síkra vetítjük, a PQ egyenest pontnak, a PQ tengely körül elfordítható sík metszeteit egyenesszakaszoknak látjuk és könnyen megszámlálhatjuk az átmetszett éleket, ami egyben a metszet oldalainak a száma.

 

Bármely X pont vetületét X'-vel jelöljük, X=A, B, ..., P, Q, ... Az egybeeső P', Q' vetület felezi A'B'-t és harmadolja A'C'-t, ezért C' a P' tükörképe B'-re, továbbá B'D'→=A'C'→ és folytatólag A'D'H'E' téglalap (az ábrákon a magasság zsugorítva). Mármost a metszet akkor és csak akkor négyszög, ha a forgó síknak S0-on levő e vetülete az A'B'F'E' téglalapból az E'F' szakaszon lép ki, magát F'-t is megengedve, viszont E'-t nem. Ugyanis csak 3 oldala van a metszetnek, ha a kilépés A'E'-n vagy éppen E'-ben történik, viszont 5, 6, majd ismét 5 oldala van ha az A'D'H'E'-ből való kilépési pont az F'G' szakaszra esik (ide értve magát G'-t is), illetve G' és H' között, végül ha H'-ben vagy a H'D' oldalon van. ‐ Így a mi síkmetszeteink további két csúcsa az EF és EG él változó R, ill. T pontja, de úgy, hogy RT∥PQ, a metszet trapéz, hiszen a fedőlappal és az alaplappal való metszésvonal párhuzamos. A trapéz magasságát az S0-on Ievő vetületben valódi nagyságban látjuk.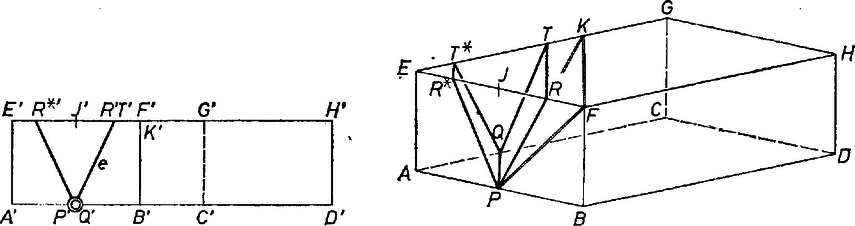
 

 

Legyen EF felezőpontja J. Ha R a JF szakasz belsejében van, és J-re való tükörképe R*, akkor a PQTR és PQT*R* trapézok magasságai egyenlők: P'R'=P'R*', a párhuzamos oldalak összegeire viszont PQ+RT>PQ+R*T*, tehát az első trapéz területe nagyobb. Minden megengedett sík beletartozik egy ilyen párba, kivéve a PQJ és PQF síkokat, így a legnagyobb területű metszetet nem adhatja PQR* típusú sík.
És mivel R-rel J-től F-ig haladva a trapézmetszet magassága is, RT is, így a párhuzamos oldalak összege is szigorúan monoton nő, azért a kérdéses metszet PQFK, ahol EK=2⋅KG.
 

 Kovács Zsolt (Szolnok, Verseghy F. Gimn., IV. o. t.)
 Horváth László (Csurgó, Csokonai Vitéz M. Gimn., IV. o. t.)
 

Megjegyzés. A talált metszet területe AB214/4.