Kezdőlap


Feladat:	F.2072	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Baumann O. , Csikós B. , Csikós Balázs , Csók T. , Dózsa G. , Erdélyi T. , Filakovszky P. , Gallai L. , Hazag T. , Helyes Balázs I. , Horváth 169 T. , Horváth 619 M. , Ivanyos G. , Józsa M. , Kamondi Z. , Kiss 361 L. , Knébel I. , Koncz K. , Kőrösi G. , Lendvay A. , Máth J. , Molnár 605 I. , Nagy 535 M. , Polhammer I. , Pyber L. , Rapai T. , Réti S. , Révész T. , Sali A. , Sas Zsuzsanna , Sóvágó Gy. , Spilkó J. , Spissich L. , Szabó 719 K. , Szegedy M. , Szőke R. , Tábori L. , Tóth 157 Csaba , Tóth Csaba , Ujj L. , Vadász Edit , Vajda Júlia , Varga T. , Vékony Cs. , Veszprémi P. , Zempléni A.
Füzet:	1977/szeptember, 10 - 13. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Vetítések, Inverzió, Gúlák, Derékszögű háromszögek geometriája, Térgeometriai bizonyítások, Alakzatok köré írt kör, Feladat
Hivatkozás(ok):	Feladatok: 1976/december: F.2072

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a gúla alapidomának egy tetszőleges csúcsa az $O$ középpontú, $r$ sugarú $k$ kör kerületén $A_{i} (i = 1,2, ...)$ , a gúla magassága $G T = m,$ és $T$ vetülete $G A_{i}$ -n $B_{i}$ (1. ábra).

1. ábra

Minden ilyen vetület rajta van a

G T

átmérő fölötti Thalész‐gömbön, így elég azt belátni, hogy a

B

pontok egy síkban vannak. Csak a nemtriviális esettel foglalkozunk,

T

nem azonos

O

-val. Ekkor a kérdéses sík nem párhuzamos az alappal, hiszen van olyan

i

j

indexpár, hogy

T A_{i} > T A_{j},

így pedig

B_{i}

magasabban van, mint

B_{j} .

(Nyilván legalább 4 csúcsa legyen az alapidomnak.)
Nem változtat az állításon, ha minden

A_{i}

-nek

T O

-ra való

A_{i}^{*}

tükörképét is alapcsúcsnak vesszük. Így

B_{i} B_{i}^{*}

merőleges a

G T O = S

szimmetriasíkra, ezért a kérdéses sík is, elég tehát azt belátnunk, hogy a

B_{i}

vetületek

S

-en levő

C_{i}

vetületei egy egyenesen sorakoznak. Evégett megmutatjuk a

T O

T G

tengelyekkel meghatározott koordináta-rendszerben, hogy

C

koordinátái között elsőfokú kapcsolat áll fenn.
Legyen

B

vetülete

T A

-ra és

T G

-re

D

, ill.

E

, továbbá

T O

-n

D

és

C

közös vetülete

F

, és

A

vetülete

H

, végül legyenek

T O

-nak

k

-n levő pontjai

U

és

V

úgy, hogy

T U < T V .

Derékszögű háromszögek, hasonlóságok felhasználásával (a tengelyirányú szakaszokat előjellel együtt értve):

\begin{matrix} T F = x = \frac{T D}{T A} T H = \frac{E B}{T A} T H = \frac{E G}{T G} T H = \frac{m - y}{m} T H; \end{matrix}

(1)

\begin{matrix} H A^{2} = T A^{2} - T H^{2} = U H \cdot H V = (T H - T U) (T U + 2 r - T H) = \end{matrix}

\begin{matrix} = 2 \cdot T H (T U + r) - T H^{2} - T U^{2} - 2 r \cdot T U, \end{matrix}

és innen

T U = u

jelöléssel

\begin{matrix} T H = \frac{T A^{2} + u (2 r + u)}{2 (r + u)}; \end{matrix}

(2)

végül a

B T D

és az

A B D

háromszögnek

A G T

-hez való hasonlóságából

\begin{matrix} T D = \frac{m y}{T A}, \frac{y}{m} = \frac{T A - T D}{T A} = \frac{T A - \frac{m y}{T A}}{T A} = \frac{T A^{2} - m y}{T A^{2}}, \end{matrix}

\begin{matrix} T A^{2} = \frac{m^{2} y}{m - y} . \end{matrix}

(3)

Ezt (2)-be, majd (2)-t (1)-be helyettesítve kapjuk állításunkat:

\begin{matrix} x = \frac{m - y}{m} \cdot \frac{\frac{m^{2} y}{m - y} + u (2 r + u)}{2 (r + u)} = \frac{(m^{2} - u^{2} - 2 r u) y + m u (2 r + u)}{2 m (r + u)} \end{matrix}

(

m

r

u

állandók).

Megjegyzés. A

k

kör és a

G

pont egy (ferde) körkúpot határoz meg. Ebben a felfogásban azt kaptuk, hogy ferde kúpnak olyan körmetszete is van, amelynek síkja nem párhuzamos az alapsíkkal, és az ezzel párhuzamos síkok szintén kört metszenek ki a kúpból. Kúpunknak az

U V G

szög felezőjén át

S

-re merőlegesen álló sík is szimmetriasíkja.

II. megoldás. Felhasználjuk a gömbre vonatkozó inverzió fogalmát és egy tulajdonságát. Legyen adott egy

O

középpontú,

r

sugarú

G

gömb.

G

-re vonatkozó inverziónak nevezzük azt a transzformációt, amely a tér egy

O

-tól különböző

P

pontjához az

O P

félegyenesnek azt a

P'

pontját rendeli, amelyre

O P' \cdot O P = r^{2}

.
Megmutatjuk, hogy az inverzió egy, a középponton át nem menő

H

gömböt egy

H'

gömbbe visz át. Legyen

H

egy pontja

P

, legyen az

O P

egyenesnek és

H

-nak a másik metszéspontja

Q

, ha ez létezik, illetve legyen

Q = P

, ha

O P

érinti

H

-t. Legyen

P'

P

-nek

G

-re vonatkozó inverz képe (2. ábra).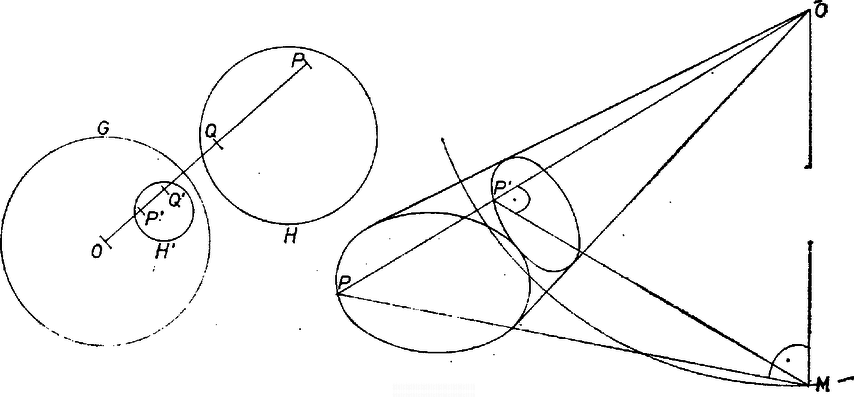

2. ábra

Legyen

q

O

-nak

H

-ra vonatkozó hatványa, azaz

O P \cdot O Q = q

. Ekkor

\begin{matrix} \frac{O P'}{O Q} = \frac{O P' \cdot O P}{O Q \cdot O P} = \frac{r^{2}}{q} . \end{matrix}

Tehát

P'

rajta lesz

H

-nak

O

középpontú,

r^{2} / q

arányú nagyítottján, vagyis

H

inverz képe a

H'

gömbön lesz, ahol

H'

H

-nak

r^{2} / q

arányú,

O

középpontú nagyítottja.
Könnyen belátható, hogy az inverzió

H

és

H'

pontjai között egy‐egy értelmű megfeleltetést létesít. Ezt tudva megmutatjuk, hogy az inverzió egy, a középponton át nem menő

k

kört egy

k'

körbe visz át. Legyenek

H_{1}

és

H_{2}

O

-n át nem menő,

k

-ra illeszkedő, különböző gömbök; ezek

G

-re vonatkozó inverz képe

H'_{1}

, illetve

H'_{2}

gömbök, így

k

inverz képe a

H'_{1}

és

H'_{2}

metszete. Az inverzió kölcsönösen egyértelmű megfeleltetést létesít

k

, valamint

H'_{1}

és

H'_{2}

közös része között, ezért a

H'_{1}

és

H'_{2}

gömbök közös része, a

k'

vonal egy kör. Tehát

k

inverz képe,

k'

, valóban kör.
Ezek után rátérünk a feladat állításának bizonyítására. Legyen

O

a gúla csúcsa,

M

a magasság talppontja,

P

az alapidom egyik csúcsa,

P'

M

-ből

O P

-re bocsátott merőleges talppontja. Az

O M P

derékszögű háromszögben

O P \cdot O P' = O M^{2}

P'

tehát

P

inverze az

O

középpontú,

O M

sugarú gömbre vonatkozólag (3. ábra). Láttuk, hogy az inverzió az alapidom köré írt kört körbe viszi,

P'

éppen ezen a körön lesz. Ezzel az állítást bebizonyítottuk.

Csikós Balázs (Budapest, Fazekas M. Gyak. Gimn., III. o. t.) dolgozata alapján

Megjegyzés. Az állítás lényegében azonos a Maklári József: Körérintési szerkesztések és alkalmazásaik c. középiskolai szakköri füzet (Tankönyvkiadó, Bp., 1970) 78. oldalán szereplő tétellel.