Feladat: F.2066 Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Cseke István ,  Csikós B. ,  Frits Gabriella ,  Horváth J. ,  Kamondi Z. ,  Knébel István ,  Lenkei P. ,  Máth J. ,  Rapai T. ,  Szabó K. ,  Székely Z. 
Füzet: 1977/április, 152 - 157. oldal  PDF  |  MathML 
Témakör(ök): Négyszög alapú gúlák, Konstruktív megoldási módszer, Térfogat, Térgeometriai számítások trigonometria nélkül, Szögfüggvények a térben, Feladat
Hivatkozás(ok):Feladatok: 1976/november: F.2066

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Csak konvex gúlákat vizsgálunk. Áttekintésünkben minden lehetséges módon összeállítunk 4 megengedett lapot a gúla palástkiterítése céljára, és minden talált esetet ellenőrizünk, ad-e valóban 4‐oldalú gúlát. Ugyanis a kiterítés ,,felvágási'' éleit összeragasztva a kapott 4‐élű testszöglet nem merev ellentétben a 3-élű testszöglettel ‐, és kérdéses, mozgatható e úgy, hogy az ,,oldalélek'' 4 végpontja egy síkba essék, illetve hogy ekkor valódi négyszög keletkezik-e. ‐ A szabályos háromszöglapokat röviden S-sel, a derékszögű, egyenlő szárú háromszöglapokat R-rel jelöljük, a gúla 4-élű csúcsát O-val, ennek vetületét az ABCD alapsíkon O'-vel, az O'O magasságot m-mel. Hosszegységnek S éleit választjuk.

 

a) Ha mind a 4 oldallapot S-nek vesszük, nyilván megfelel a szabályos négy oldalú gúla. De azt is be kell látnunk, hogy más lehetőség ekkor nincs. Mind a négy oldalél 1, tehát A, B, G, D az O körüli, 1 sugarú gömbnek és az alapsíknak a metszésvonalán vannak. Ez kör, tehát az alapidom húrnégyszög. És mivel mindegyik alapél hossza is 1, az alap csak a szabályos négyszög lehet. ‐ (Alább még néhányszor kapunk hasonlóan húrnégyszöget, azt már indokolás nélkül csak kimondjuk; más ismétlődő elemeket is csak először részletezünk.) ‐
Tovább az R-lapok számát 1-esével növeljük.
b) Ha 1 oldallap R ‐ legyen ez a DOA lap ‐, akkor a kiterítés 3 db S-ből álló, összefüggő ,,blokk''-ján OA=OD, tehát R csak két egyenlő oldalával, a két befogójával illeszkedhet közéjük, DOA∢=90∘. Az alap ‐ ha létezik ‐ csak húrnégyszög lehet, benne AD=2, a többi oldal 1, és a köré írt kör O'A=r sugara kisebb, mint 1. Ugyanis 1 sugarú körben fölmérve az 1, 1, 1, 2 húrokat, csak 3⋅60∘+90∘ ívet vágnánk le, nem záródnék a négyszög. Könnyű utánaszámítani, hogy az alapnégyszög valóban így jön létre. így az 00'=1-r2 magasság pozitív, a gúla létrejön (1. ábra, palást és vetület az alapon, az AD, BC élek közös felező merőleges síkja szimmetriasík).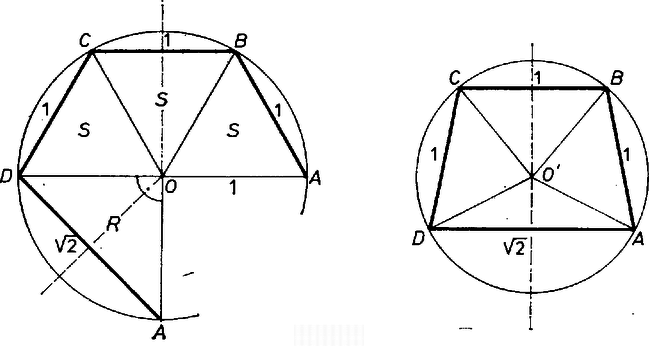
 

 

1. ábra
 

‐ Tovább is mindaddig úgy beszélünk, hogy a palástból keletkezik gúla, míg csak ez meg nem cáfolódik.
c) Két db R-lap esetében az oldallapok ciklikus sorrendje lehet SSRR és SRSR.
c1) Az SRSR sorrend mellett a két nem szomszédos S-lap révén minden oldalél hossza 1, az R-ek itt is csak a derékszögükkel illeszthetők O-ba, átfogóik az alapra jutnak, az alapidom húrparalelogramma, azaz húrtéglalap 1 és 2 oldalakkal, r=3/2, a gúla létrejön (2 szimmetriasíkja is van).
Az SSRR sorrend mellett betűzzük az SS blokkot OBCD-vel. Ekkor az R-lapok közös OA élének hossza vagy 1, vagy 1/2 vagy 2, aszerint, hogy a derékszög csúcsa mindkettőben O, illetve A, illetve ha külön vannak B-ben és D-ben (2‐4. ábrák). Ezért a palást finomabb leírásában az R jelek közé odaírjuk OA-nak éppen vizsgált hosszát.
c2) Az S, S, R, (1), R esetben is húrnégyszög az alap, pontosabban húrdeltoid, oldalai 1 és 2 tehát a két egyenlő szöge derékszög, tengelyének hossza 3, ismét m>0 (2. ábra, AOC szimmetriasík).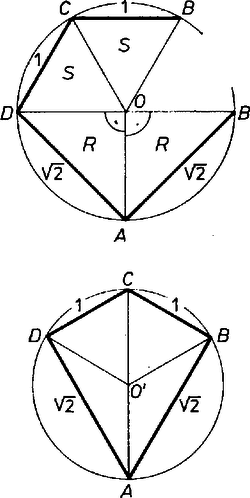
 

 

2. ábra
 

c3) Az S, S, R, (1/2), R esetben a palást nem 4, hanem 3-oldalú gúlává áll össze. Ugyanis jelölésünk szerint OA merőlegesen áll AB-re és AD-re, tehát az ABD alapsíkra is, ezért O' azonos A-val. Továbbá OB=OC=OD alapján a B, C, D kör sugara O'B=AB=1/2, ugyanekkora AC is, ekkor pedig BC=1 alapján BAC∢=90∘=DAC∢, A felezi a BD szakaszt, az OAB, OAD lapok egy síkba esnek (3. ábra).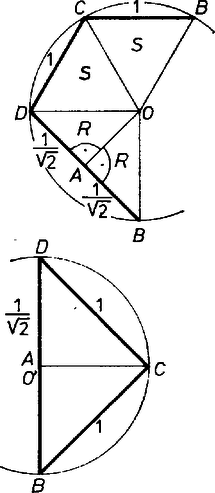
 

 

3. ábra
 

c4) Az S, S, R, (2), R esetben az alap 1 oldalú rombusz, O' a B, C, D csúcsokon átmenő kör középpontja, az ABO és ADO derékszögek vetületei derékszögek. Ezért AO'>O'B=O'C<AC2<AB+BC2=1, a BCD kör sugara <1, a gúla létrejön (4. ábra, ACO szimmetriasík; egyébként könnyen adódik, hogy ekkor OBCD szabályos tetraéder, és 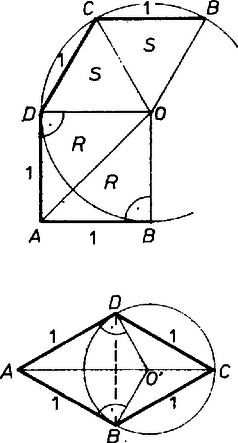OA⊥OC).
 

 

4. ábra
 

d) Három db R-lap közül a két szélső: R1 és R3 az egyetlen S-hez egyformán vagy az átfogójával csatlakozik, vagy egyik befogójával, csak így lehet egybevágó ez a két lap.
d1) Az R1, (átf.), S, (átf.), R3 esetben a két még szabad oldalél befogó, tehát egyenlők, következésképpen R2-nek a derékszöge jut O-ba. Így az alapélek 1, 12, 1, 12, az alap csak paralelogramma lehet, pontosabban téglalap, mert a palást szimmetrikus összeállítása alapján a gúla is szimmetrikus az 1-es alapélek felező merőleges síkjára. Így R2 oldaléleinek vetületei éppen az átfogójára esnek, rövidülnek, tehát a gúla létezik, az R2 lap merőleges az alapra (5. ábra, 1 szimmetriasík).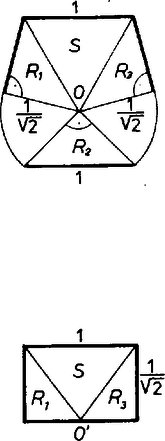
 

 

5. ábra
 

Az R1, (bef.), S, (bef.), R3 elindulásban e két R-lap derékszögű csúcsának a helyzetére 2 lehetőség veendő figyelembe (6‐7. ábrák). Legyen ugyanis S=OAB, akkor vagy mindkét R-nek O-ba esik a derékszögű csúcsa, vagy az egyiké O-ba, a másiké ‐ mondjuk A-ba. (Nem eshetnek A-ba és B-be, különben ugyanis OC=OD=2 lenne, viszont a hátra levő R2-nek csak egy oldala ekkora.)
d2) Az első változatban R2 ismét csak a derékszögével illeszkedhet O-ba, az alap húrnégyszög, 3 oldala 2, a negyedik 1. Ismét r<1, mert r=1 mellett a négy oldal csak 330∘-ot fedne le a kerületből, a gúla létezik (6. ábra, 1 szimmetriasík).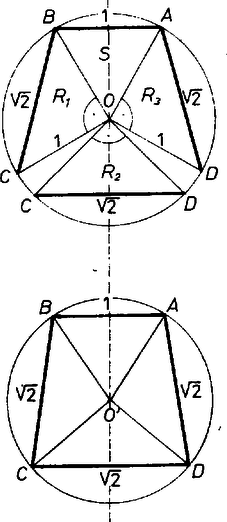
 

 

6. ábra
 

d3) A második változatban OC=1 és OD=2, így R2=COD beillesztése egyértelmű. Az alap 3 oldala 1, a negyedik 2, de a négyszög nem húrnégyszög és nem is szimmetrikus, ezért valamivel többet kell számolgatnunk, nincs-e ellentmondás ebben a szokatlan esetben. Felhasználjuk, hogy O' az A, B, C kör középpontja, másrészt hogy O'CD és O'AD derékszögek, tehát O'ADC húrdeltoid. Jelöljük az O'DA szöget δ-val, ekkor AO'C∢=180∘-2δ, ABC∢=90∘-δ, és az ACB, ACD háromszögekből egybevetéssel, a cosinustétel alapján, valamint mindjárt trigonometrikus azonosságokat is figyelembe véve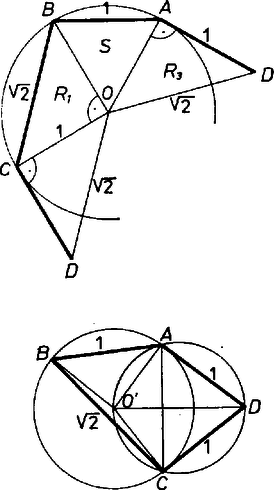
AC2=1+2-22sinδ=1+1-2cos2δ=4sin2δ.
Ez másodfokú egyenlet sinδ-ra, itt csak a pozitív gyök használható, és arra
sinδ=7-122<12mert7-12<9-12=1.
Ezért δ>45∘, az A, B, C kör sugara ADtgδ<1, így pedig m>0, a gúla létezik (7. ábra).
 

 

7. ábra
 

e) Végül, ha mind a 4 oldallap R, két próbálkozásunk sikertelen. Ha O-ban mind a 4 lapot a derékszögével fogjuk össze, a palást 0 magasságú gúlát ad, hiszen az alap mindegyik oldala 2, és így r=1; ha pedig O-ban 45∘-os szögeket illesztünk össze, az ,,oldaléljelöltek'' váltakozva 1 és 2 hosszúak; és ha OA=OC=1, akkor az ,,alap'' AC átlójának O-tól való távolsága kisebb, mint 1, a BD átlóé pedig nagyobb, mint 1, mert a 3-élű (O)BAD testszögletben BOD∢<BOA∢+AOD∢=90∘, így csak az OAC háromszög szakasszá elfajulása esetében lehet mind a kettő 1 (gyermekcsákó készítése újságpapírból).
Az utolsó lehetőség viszont ismét sikeres, ez adja tehát a feladat második része szerint végzendő számítás tárgyát: amikor 0-ban a szögek 90∘, 90∘, 45∘, 45∘; az utóbbi kettő legyen az OD él két oldalán. Az alap deltoid, szimmetriatengelye BD, és ezen van O' is, mint az A, B, C kör középpontja. m-et fogjuk meghatározni, és ezzel fejezzük ki a további számításhoz szükséges BD, AC átlókat is (8. ábra).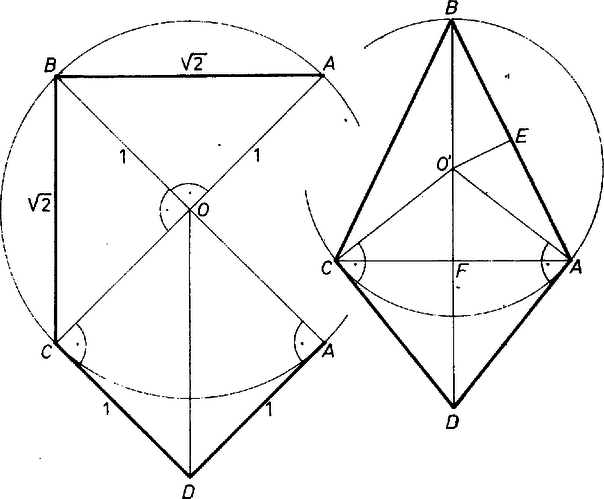
 

 

8. ábra
 

Jelöljük az átlók metszéspontját F-fel, AB felezőpontját E-vel. Így
OE=EA=12,O'E=12-m2,O'B=O'A=1-m2O'D=2-m2,


az AFB, O'EB háromszögek hasonlóságából
AF=O'EABO'B=1-2m21-m2=1-m21-m2,
továbbá a DFA, O'FA derékszögű háromszögekből
DF=m1-m2,illetveO'F=m21-m2.
Most már a nyilvánvaló DF+FO'=DO' egyenlőségből:
m+m21-m2=2-m2,m3+2m2-1=0.



Könnyű látni, hogy m=-1 kielégíti ezt az egyenletet, tehát a bal oldal szorzatra bontható úgy, hogy az egyik tényező m+1:
(m3+m2)+(m2-1)=(m+1)(m2+m-1)=0.
Számunkra csak az
m2+m-1=0(1)
egyenlet pozitív gyöke felel meg:
m=5-12(2)

Felismerjük ebben az ,,aranymetszés'' szerint kettéosztott egységszakasz nagyobbik részének a mértékszámát ‐ amint már (1)ben. is felismerhetjük a megfelelő egyenletet ‐, és erről eszünkbe jut, hogy több ezzel kapcsolatos számkifejezés jelentősen egyszerűsíthető. Itt is ilyen szerencsénk lesz. Mivel (1)ből 1-m2=m és 1-m=m2, továbbá 2-m2=1+m, ezért a fentiekből az átlók darabjaira, majd a V térfogatra
O'B=m,O'D=1+m,AF=1-m=m,3V=O'O⋅AF⋅BD=m2(1+m+m).



Tovább egyszerűsödik kifejezésünk, ha kétszer alkalmazzuk a (2)-ből a számláló gyöktelenítése útján adódó következő kifejezést:
1+m=5+12=25-1=1m,3V=m2(1m+m)=mm(1+m)=m,V=m3=5-118=0,262térfogategység.


(Kis számítógéppel végrehajtva kényelmesebb, ha csak egy helyen osztunk, ezért vittük be az osztót.)
Ezzel a feladat második részét is befejeztük. Mondjuk ki, hogy az első kérdésre 9 megfelelő gúlát találtunk.
 

Cseke István és Knébel István
(Budapest, József A. Gimn., IV. o. t.) dolgozataiból, kiegészítéssel

 

Megjegyzések. 1. Figyeljünk fel az iménti meglepően egyszerű AF=m részeredményre. Az ilyen megállapítás mögött nemegyszer egyszerű magyarázat is áll. Tükrözzük gúlánkat az alapsíkra és jelöljük O képét O*-gal (9. ábra). Ekkor az OBO*D deltoid egybevágó az alappal, a csúcsok CDAB körüljárás szerinti megfeleltetésével, vagyis B és D szerepcseréjével, hiszen oldalaik és tengelyük rendre egyenlők. ‐ Ezzel megmagyaráztuk: nem jutott hibás eredményre, aki FB-re használta fel O'D fenti kifejezését m kiszámításában ‐ csak hát meg kellett volna indokolnia ezt a lépést.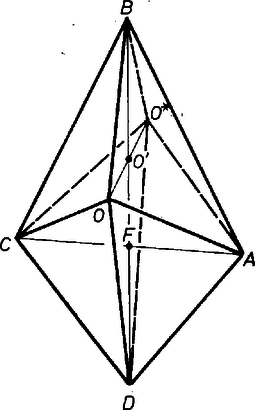
 

 

9. ábra
 

2. A 9. ábrán kapott poliéder B és D csúcsában éppen olyan 4-élű szögletek vannak, amilyen utolsó előtti próbálkozásunkban szerepelt, de nem sikerült egy síkba hozni az A, O, C, O* pontokat. Egyes kristályosztályokban is föllép az itt látható ,,forgótükrözéses'' szimmetria: a test fedésbe jut önmagával BD körüli negyedfordulat és a tengely felező merőleges síkjára való tükrözés együttes alkalmazásával.
Hasonlóan többi gúláink tükrözésével is az alap csúcsaiban a már vizsgált 4-élű szögletek valamelyike adódik, de a 4 élvégpont többnyire nincs egy síkban.