Kezdőlap


Feladat:	F.2060	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Baksai Róbert
Füzet:	1977/február, 68 - 69. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Természetes számok, Térgeometriai bizonyítások, Térgeometriai számítások trigonometria nélkül, Tetraéderek, Feladat
Hivatkozás(ok):	Feladatok: 1976/október: F.2060

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. A csonkagúlák helyett az eredeti gúla csúcsa és az alapjával párhuzamos síkok által meghatározott gúlákat vizsgáljuk. A síkoknak a közös csúcstól mért távolságai legyenek $m_{1}, m_{2}, ..., m_{24} (m_{24} = m$ , az eredeti gúla magassága). Ha az eredeti gúla térfogata $V$ , akkor az $m_{i}$ magasságú gúláé a felosztás szerint 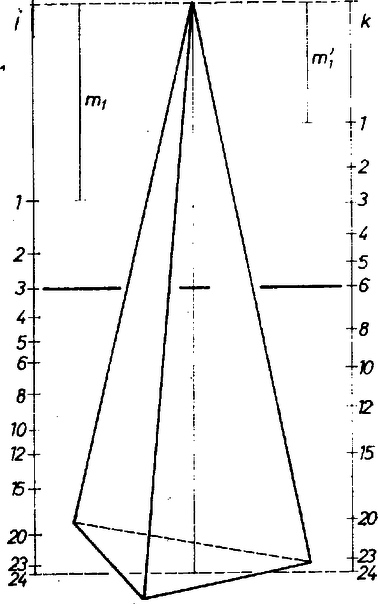$V_{i} = \frac{i}{24} V$ , tehát $V_{i} / V = i / 24, i = 1, 2, ..., 23$ .

A gúlák megfelelő lapjait alkotó háromszögek, ill. az alapsokszögek hasonlóak, a megfelelő élek aránya

m_{i} / m

, ezért

V_{i} / V = m_{i}^{3} / m^{3}

. A két egyenlőségből következik, hogy

\begin{matrix} m_{i} = m \sqrt[^{3}]{\frac{i}{24}} . \end{matrix}

A második felosztás esetén az

m'_{k}

magasságú gúla palástfelszíne

F_{k} = \frac{k}{24} F

, ahol

F

az eredeti gúla palástfelszíne,

k = 1, 2, ..., 23

, így

F_{k} / F = k / 24

. A hasonlóság alapján

F_{k} / F = m'_{k}^{2} / m^{2}

, amiből

m'_{k} = m \sqrt[]{\frac{k}{24}}

.
A két síkhalmaznak akkor van közös síkja, ha valamilyen

i, k

számpárra teljesül, hogy

m_{i} = m'_{k}

. Ez azt jelenti, hogy

\begin{matrix} \sqrt[^{3}]{\frac{i}{24}} = \sqrt[]{\frac{k}{24}}, azaz 24 i^{2} = k^{3} . \end{matrix}

Mivel

24 = 3 \cdot 2^{3}

, azért az

i = 3, k = 6

számpárra teljesül a feltétel: az első felosztás harmadik síkja egybeesik a második felosztás hatodik síkjával. Ez a sík félmagasságban vágja ketté a gúlát, fölötte van a

V

térfogat

{(\frac{1}{2})}^{3} = \frac{3}{24}

-ed része és az

F

palást felszín

{(\frac{1}{2})}^{2} = \frac{6}{24}

-ed része.

2. Ha a gúlát

n

síkkal osztjuk a két elv szerint részekre, akkor az előzőekhez hasonlóan feltételként az

\begin{matrix} (n + 1) i^{2} = k^{3}, 1 \leq i, k \leq n \end{matrix}

egyenletre jutunk. Amely

(n + 1)

értékekre van megoldás, a kétféle

n

-elemű síkhalmaznak van közös síkja.
Ha mármost

(n + 1)

törzstényezős felbontásban nem fordul elő harmadik vagy annál magasabb hatvány, akkor az egyenletnek nincs megoldása az

1 \leq i, k \leq

\leq n

követelmény mellett. Ekkor ugyanis

(n + 1)

felbontásban minden előforduló prímszám kitevője vagy

α = 1

, vagy

α = 2

, és ezt

i^{2}

-nek kell (

k^{3}

céljára)

3

-ra vagy

3

valamely többszörösére emelnie,

α = 1

-ről legalább

3

-ra,

α = 2

-ről pedig legalább

6

-ra, hiszen

i^{2}

-ben páros a kitevő. Így

i

-nek tartalmaznia kell

(n + 1)

-nek minden prímtényezőjét legalább akkora kitevővel, mint maga

(n + 1)

, ami csak

i \geq n + 1

mellett lenne lehetséges.
Ha viszont

n + 1 = q \cdot p^{3}

, ahol

p > 1

és

q

természetes számok, akkor pl. az

i = q

k = q \cdot p

számpár minden

q = 1, 2, 3, ...

mellett megoldása az egyenletnek. A

100

alatti köbszámok

8, 27, 64

, ezért a megfelelő

n

értékek:

\begin{matrix} 7, 15, 23, 26, 31, 39, 47, 53, 55, 63, 71, 79, 80, 87, 95. \end{matrix}

Már itt észrevesszük, hogy az

n = 63

-at kétféleképpen is megkaptuk:

63 =

= 8 \cdot 2^{3} - 1 = 1 \cdot 4^{3} - 1

, tehát itt két közös síkot kapunk:

i = 8, k = 16

és

i = 1, k = 4

Baksai Róbert (Győr, Révai M. Gimn. IV. o. t.)