Kezdőlap


Feladat:	F.2059	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Kamondi Zoltán
Füzet:	1977/február, 67 - 68. oldal		PDF \| MathML
Témakör(ök):	Alakzatok szimmetriái, Tengelyes tükrözés, Vetítések, Egyenesek egyenlete, Feladat
Hivatkozás(ok):	Feladatok: 1976/október: F.2059

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Keressük meg először a kérdéses egyenest, föltéve persze, hogy az állítás igaz. Ehhez $M$ -et $3$ speciális helyzetben vesszük föl.

M

-et

A_{1}

-gyel azonosnak véve az első merőleges maga az

m

; ez átmegy

C

-n, a második merőleges fix pontján, így a második merőlegest meg sem kell rajzolnunk, ebben a fölvételben

N_{I}

azonos

C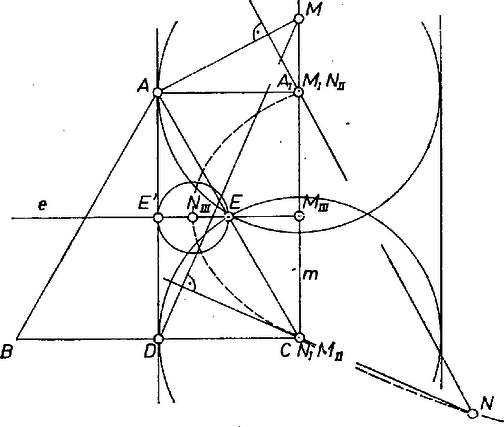

-vel.

II. Hasonlóan, ha

M

-et,

C

-ben vesszük, a második merőleges azonos

m

-mel és

N_{II}

, azonos

A_{1}

-gyel. Így

N_{I}

és

N_{II}

, egymás tükörképei az

A_{1} C

szakasz

e

felező merőlegesére mint tengelyre, amelyen

E

, a körök fix pontja is rajta van. A két kör sugara egyenlő,

2

közös érintőjük van,

A D

és ennek eltoltja a

\vec{B C}

-ral.

III. Vegyük harmadszor

M

helyét

m

és

e

metszéspontjában, ekkor a két merőleges irányát meghatározó

M_{III} A

és

M_{III} D

egyenesek is tükrösek

e

-re. Így

N_{III}

e

-n adódik, és az

N_{III} M_{III} A_{1}

és

M_{III} A_{1} A

derékszögű háromszögek hasonlósága alapján

\begin{matrix} N_{III} M_{III} = \frac{M_{III} A_{1}^{2}}{A_{1} A} = \frac{3 B C}{8}, \end{matrix}

vagyis

N_{III}

felezi az

E E'

szakaszt, ahol

E'

E

vetülete

A D

-re, az

M_{III}

-hoz tartozó kör az előbbi két jelöltünk közül

A D

-t érinti (

E'

-ben), erre kell tehát bizonyítanunk az állítást, ami egyébként most már így is kimondható:

N

rajta van azon a parabolán, amelynek fókusza

E

és vezéregyenese

A D

2. Válasszuk koordináta-rendszerünk origójául

E'

-t, és legyenek

E

koordinátái

(\frac{1}{2}; 0)

, ekkor

A (0, h)

D (0, - h)

A_{1} (1, h)

C (1, - h)

, ahol

h = \sqrt[]{3} / 2

, továbbá

M

tetszőleges helyzete

(1, t)

, ahol

t \neq 0

\pm h

, (ezekre már tudjuk az állítás helyességét).

A M

iránytangense

t - h

, így az első merőleges egyenlete:

\begin{matrix} y = h - \frac{1}{t - h} (x - 1) . \end{matrix}

Ebből a második merőleges egyenletét úgy kapjuk, hogy

h

helyére

(- h)

-t írunk:

\begin{matrix} y = - h - \frac{1}{t + h} (x - 1) . \end{matrix}

Metszéspontjuk koordinátái:

\begin{matrix} N (t^{2} - h^{2} + 1; \end{matrix}

és az

N E

sugár négyzete:

\begin{matrix} r^{2} = {(t^{2} + \frac{1}{4} - \frac{1}{2})}^{2} + {(- t)}^{2} = t^{4} + \frac{1}{2} t^{2} + \frac{1}{16} = {(t^{2} + \frac{1}{4})}^{2}, \end{matrix}

vagyis a sugár egyenlő

N

abszcisszájával.
Ez pedig azt jelenti, hogy a kör ,,bal szélső'' (azaz legkisebb abszcisszájú) pontja éppen rajta van az ordinátatengelyen, a kör érinti

A D

-t. Állításunkat bebizonyítottuk.

Kamondi Zoltán (Zalaegerszeg, Zrínyi M. Gimn., III. o. t.)