Kezdőlap


Feladat:	F.2058	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Ármós L. , Baksai R. , Balázs I. J. , Bartke I. , Benkő T. , Berényi P. , Csapó Ildikó , Csikós B. , Erdélyi T. , Etlinger J. , Filakovszky P. , G. Horváth Á. , Goór Cs. , Gubics J. , Homonnay G. , Ivanyos G. , Jakab Emma , Kardos Z. , Kelemen Terézia , Kiss L. , Knébel I. , Kőkúti R. , Koncz K. , Kozma L. , Laszip A. , Máth J. , Merth Z. , Nagy 691 T. , Nemes I. , Németh 892 R. , Németh E. , Nieder Ildikó , Papp 513 A. , Pósafalvi A. , Rapai T. , Réti S. , Rosanics Gy. , Slezák T. , Spilkó J. , Szabó 719 K. , Sörös G. , Tábori L. , Tóth Annamária , Tóth Cs. , Vancsa I. , Vándor T. , Végh F. , Verő Mária
Füzet:	1977/február, 65 - 66. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Négyszögek geometriája, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1976/október: F.2058

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Jelöljük a $φ$ szög csúcsát $P$ -vel, és a számpélda $A B = 2 \cdot C D$ összefüggésére gondolva, válasszuk úgy a betűzést, hogy $P D < P A$ legyen, így a konvexség alapján $P C < P B$ is teljesül. (Lényegében azonos a meggondolás a $P D > P A$ kiindulásból is.) Eszerint a $P D C$ háromszög benne van a $P A B$ háromszögben, a szögfelezőkre tekintettel $M$ a $P A B$ háromszögbe beírt kör középpontja, $N$ pedig a $P D C$ háromszög $D C$ oldalához hozzáírt külső érintő kör középpontja, tehát mindkettő rajta van a háromszögek közös $P$ csúcsánál levő szög felezőjén, és 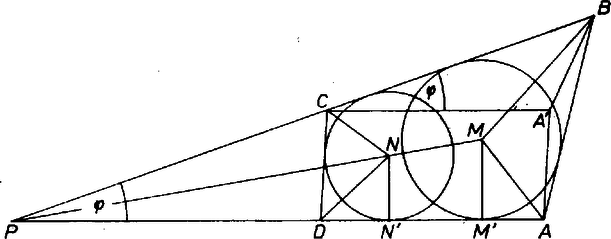$M N = | P M - P N |$ .

Jelöljük

M

-nek és

N

-nek a közös

P A

oldalegyenesen levő vetületét, az említett körök érintési pontját

M'

-vel, ill.

N'

-vel, ekkor

\begin{matrix} M N = \frac{M' N'}{cos φ / 2} = \frac{| P M' - P N' |}{cos φ / 2}, \end{matrix}

és itt ‐ mint az érintési pontokig terjedő oldalszakaszokra ismeretes ‐

\begin{matrix} P M' = \frac{1}{2} (P A + P B - A B) = \frac{1}{2} (P D + D A + P C + C B - A B), \\ P N' = \frac{1}{2} (P D + P C + C D), \end{matrix}

ennélfogva

\begin{matrix} M N = \frac{1}{2 cos \frac{φ}{2}} \cdot | (D A + C B) - (A B - C D) | . \end{matrix}

Eredményünknek az a speciális esete, amikor

M

és

N

egybeesik,

M N = 0

, vagyis egyenlő távolságra vannak az

A B C D

négyszög mindegyik oldalától éppen azonos az

A B C D

-be beírt kör létezésének ismert szükséges feltételével (ami ‐ mint sokan tudják ‐ egyszersmind elegendő feltétel is).

2. A számpéldában először azt az esetet vesszük, ha

φ

hegyesszög, vagyis

\begin{matrix} cos φ = + 0, 96; \end{matrix}

és

\begin{matrix} M N = \frac{\sqrt[]{2}}{2, 8} | 75 + 100 - 70 - 35 | = 25 \sqrt[]{2} \approx 35 egység . \end{matrix}

Ha viszont

φ

-t tompaszögnek próbáljuk venni:

\begin{matrix} cos φ = - 0, 96, akkor cos \frac{φ}{2} = \frac{0, 2}{\sqrt[]{2}}, \end{matrix}

ebből

M N = 175 \sqrt[]{2} \approx 247, 5

adódik, és ez lehetetlen, hiszen négyszögünk

A C

átlója kisebb, mint az

A D + D C = 110

és az

A B + B C = 170

összegek kisebbike, azaz mint

110

, és a

B D

átló kisebb, mint

D A + A B = 145

és

B C + C D = 135

kisebbike,

135

, tehát négyszögünk nem tartalmazhat

110

és

135

nagyobbikánál hosszabb szakaszt.

Megjegyzés. Csekély többletszámítással az is adódik, hogy négyszögünk trapéz, a

C D

oldal a

P A B

háromszögnek

B A

-val párhuzamos középvonala. Eljuthatunk erre úgy, hogy azt az eljárást követjük számítással, ahogyan adatainkból és a

0^{\circ} < φ < 90^{\circ}

mellékfeltevésből az

A B C D

négyszöget szerkesztenénk (

D A

eltolása a

C A'

helyzetbe,

B C A'

háromszög,

B A' A

háromszög az oldalaiból, és

A' C

eltolása

A D

-be; ezúttal

B A' + A' A = B A

-nak adódik). A

P A B

háromszög hasonló a 2028. feladatban vizsgált háromszöghöz (KÖMAL 53. köt. (1976) 123. old.).