Kezdőlap


Feladat:	F.2053	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1977/január, 11 - 14. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Húrnégyszögek, Feladat
Hivatkozás(ok):	Feladatok: 1976/szeptember: F.2053

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Két hegyesszög összege nem érheti el a $180^{\circ}$ -ot, amennyi bármely konvex húrnégyszögben két szemben fekvő szög összege, ezért a két adott értékű hegyesszög négyszögeink valamelyik oldalának végpontjaiban van. Válasszuk úgy az $A B C D = N$ négyszög betűzését, hogy ez az oldal $A B$ , és az adott két szög $α$ , $β$ legyen úgy, hogy

\begin{matrix} 90^{\circ} > B A D ∢ = α \geq β = A B C ∢ > 0^{\circ} . \end{matrix}

Tartsuk

k

(és

N

) síkját függőlegesen és az

A B

oldalt vízszintesen úgy, hogy

C

és

D

följebb legyenek, mint

A

. Ekkor

k

tetszőleges pontját

A

-nak választva, kijelölhetjük

B

C

és

D

helyzetét, az utóbbi két szögpont azonban nem mindig jön létre, és ha létrejönnek, akkor sem mindig konvex négyszöget ad az önmagában záródó

A B C D A

útvonal. Feladatunk első része éppen ennek vizsgálata, ebből azután kiadódnak az egyes oldalak keresett korlátai.
Az előzőkkel az első három oldal irányain túl a

D C

oldal irányát is meghatároztuk, hiszen a

D

-nél levő külső szög

β

, és így a

D C

oldal

(α - β)

szöggel hajlik a vízszintes

A B

-hez. Így mind a

4

oldal felezőpontja csupán az illető irányra merőleges átmérőn mozoghat (pontosabban azoknak is csak 1‐1 szakaszán). Célszerű ezt a

4

átmérő kijelölése után így mondani:

N

egyes oldalainak két végpontja mindig egymás tükrös párja a megfelelő átmérőre nézve.
2. Válasszuk

A

kiinduló helyzetéül

k

vízszintes átmérőjének

A_{0}

jobb oldali végpontját, vegyük hozzá a

B_{0}

C_{0}

D_{0}

pontokat, és vizsgáljuk először az olyan

α

β

értékpárok esetét, amelyek mellett a két szög

A_{0} D_{0}

és

B_{0} C_{0}

ferde szárai a

k

belsejében vagy éppen a

k

-n levő

M_{0}

pontban metszik egymást (1. ábra).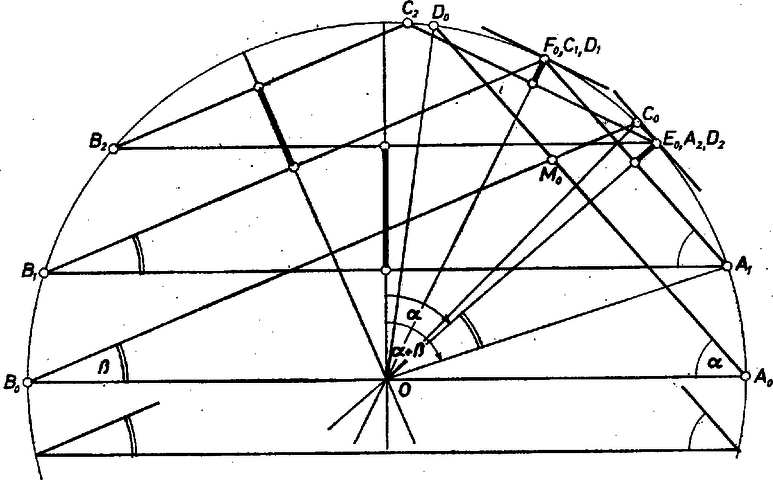

1. ábra

Akkor ilyen a helyzet, ha

\begin{matrix} A_{0} M_{0} B_{0} ∢ = 180^{\circ} - (α + β) \geq 90^{\circ}, azaz ha α + β \leq 90^{\circ} . \end{matrix}

Ekkor az

A_{0} D_{0}

és

B_{0} C_{0}

"oldalak'' szétválasztják egymás végpontjait,

N_{0}

hurkolt négyszög, illetve

α + β = 90^{\circ}

esetén

C_{0}, D_{0}

és

M_{0}

egybeesése folytán derékszögű háromszög, semmiképpen nem a "mi négyszögünk''. Viszont már így is kijelölhetjük az oldalirányokra merőleges átmérőket; pontosabban mondva, elég lesz az

A D

és a

D C

oldalra merőleges átmérő

E_{0}

, illetve

F_{0}

felső végpontja, ezt nyilván az

A_{0} D_{0}

, illetve a

D_{0} C_{0}

ív felezőpontja adja meg.
Ilyen marad a helyzet akkor is, ha

A

-t lefelé toljuk

k

alsó pontjáig, és egy darabig akkor is, ha

A_{0}

-tól fölfele toljuk. Az eddigi hurkoltság, (

C_{0}

és

D_{0}

nem megfelelő sorrendje) akkor szűnik meg, amikor az egymással szemben haladó

C

és

D

összetalálkoznak

F_{0}

-ban; nevezzük ezt négyszögünk (1-es indexű)

N_{1}

helyzetűnek, bár

C_{1}

és

D_{1}

egybeesése miatt még ez is csak háromszög. De ha az ehhez tartozó

A_{1}

-től ‐ ami

F_{0} \equiv D_{1}

-nek

E_{0}

-ra vonatkozó tükörképe ‐ bármily kicsivel is feljebb vesszük

A

-t, megfelelő négyszöget kapunk.
Tovább tolva

A

-t,

A

és

D

találkoznak össze

E_{0}

-ban, négyszögünknek ez az

N_{2}

helyzete már ismét csak háromszög, és innen kezdve az

A D

félegyenes meredekebb, mint

k

-nak

A

-beli érintője, tovább tehát nincs mit keresnünk. (Ha

β = α

, akkor

A

és

D

-vel egyidejűen

B

és

C

összetalálkoznak,

β < α

esetén azonban ez nem áll be.) Ezek szerint

D

N

-nek a "kényes'' pontja.
Összefoglalva az eddigieket:

N_{0}

csúcsai és

E_{0}

F_{0}

, kijelölése után akkor kapunk konvex (és előírt irányú oldalakkal bíró) négyszöget, ha

D

-t az

E_{0} F_{0}

ív belsejében vesszük fel ‐ és ekkor tovább

E_{0}

-ra,

F_{0}

-ra való tükrözéssel kapjuk

D

-ből

A

-t,

C

-t, végül

A

-val "egy magasságban''

B

-t. Egyben az oldalhosszúságok keresett korlátai, míg a háromszöggé elfajult

N_{1}

és

N_{2}

között haladunk:

\begin{matrix} B_{1} A_{1} > B A > B_{2} A_{2} = B_{2} E_{0}, & A_{1} D_{1} > A D > 0, \\ 0 < D C < D_{2} C_{2} = E_{0} C_{2}, & F_{0} B_{1} = C_{1} B_{1} > C B > C_{2} B_{2}, \end{matrix}

itt

B_{1}

B_{2}

A_{1}

-gyel,

A_{2}

-vel egy magasságban levő pontja

k

-nak,

C_{2}

pedig

E_{0}

tükörképe

F_{0}

-ra. Egyenlőség sehol nincs megengedve. Az oldalak tengelyeinek figyelembe jövő szakaszait az 1. ábrán vastagítottuk.
3. Könnyű belátni, hogy az

\begin{matrix} A_{1} B_{1}, B_{1} C_{1}, C_{1} A_{1}, A_{2} B_{2}, B_{2} C_{2}, C_{2} D_{2} \end{matrix}

húrnak az

O

középpontból vett látószöge rendre

\begin{matrix} 2 (α + β), 2 α, 2 β, 2 α, 2 (α - β), 2 β, \end{matrix}

ennélfogva a vizsgált esetben

\begin{matrix} sin (α + β) > B A > sin α, sin β > A D > 0, \\ 0 < D C < sin β, sin α > C B > sin (α - β), \end{matrix}

és

B A

esetére a kiindulás biztosítja, hogy

sin (α + β) > sin β

.
4. Hasonlóan tárgyalható az olyan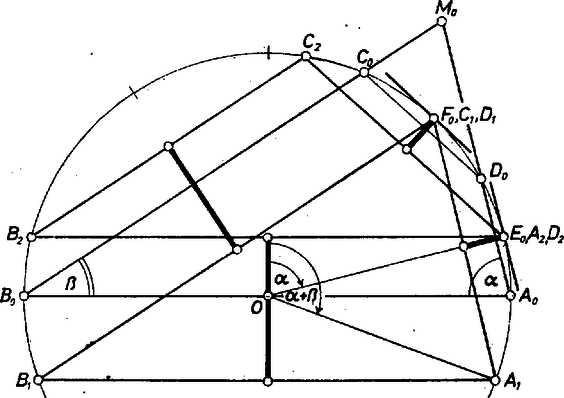

α

β

értékpárok esete, amelyekre

M_{0}

k

-n kívül adódik,

α + β > 90^{\circ}

(2. ábra).

2. ábra

Eltérés csak az, hogy ekkor mindjárt

N_{0}

a mi négyszögünk, továbbá

C

-nek és

D

-nek

E_{0}

-ban való összetalálkozását

A

-nak

A_{0}

-ból lefelé való elmozdítása okozza,

A B

A_{0} B_{0} = 1

értéktől az

A_{1} B_{1}

és

A_{2} B_{2}

húrok kisebbikéig csökkenhet (az egyenlőség kizárásával), és itt

sin (α + β) ⋛ sin α

mindegyike lehetséges.
Ehelyett inkább számítással, formálisan vizsgáljuk pontjaink helyes sorrendjének feltételeit.
Körünk

P

pontjait az irányított

A_{0} O P

szöggel jellemezzük. Legyen

A

ilyen koordinátája

φ

, akkor

B

koordinátája

180^{\circ} - φ

, ahol

- 90^{\circ} < φ < 90^{\circ}

, továbbá

D O B ∢ = 2

D A B ∢ = 2 α

A O C ∢ = 2

A B C ∢ = 2 β

alapján

C

és

D

koordinátája

φ + 2 β

, ill.

180^{\circ} - φ - 2 α

. (

B

C

és

D

tehát az

A

-éval egyenlő sebességgel mozognak,

A

és

C

az egyik,

B

és

D

a másik forgási irányban.) Ahhoz, hogy

A B C D

konvex négyszög legyen, szükséges és elegendő, hogy álljon (jelképesen

A < D < C < B

, azaz)

\begin{matrix} φ < 180^{\circ} - φ - 2 α < φ + 2 β < 180^{\circ} - φ . \end{matrix}

Az első kettőből

φ < 90^{\circ} - α

, emiatt kell

A

-nak az

E_{0} \equiv A_{2}

alatt maradnia, hiszen (jelképesen)

\begin{matrix} E_{0} = \frac{1}{2} (A + D) = 90^{\circ} - α . \end{matrix}

Ez mindig

k

felső felén van. A másodikból és a harmadikból

φ > 90^{\circ} - α - β

, és itt a jobb oldal

A_{1}

koordinátája; hiszen

\begin{matrix} A_{1} = 2 E_{0} - F_{0} = (A + D) - \frac{D + C}{2} = \frac{1}{2} (2 A + D - C) = 90^{\circ} - α - β . \end{matrix}

(Ez lehet

A_{0}

fölött is, alatta is.)
Az utolsó két koordináta közti egyenlőtlenség nem hoz új korlátozást:

φ < 90^{\circ} - β

, ez

β \leq α

és

φ < 90^{\circ} - α

következtében teljesül.
Mint látjuk, e számítás elemzése nem teheti fölöslegessé

α + β

és

90^{\circ}

nagyságviszonyának figyelembevételét.