Kezdőlap


Feladat:	F.2052	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1977/január, 10 - 11. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Derékszögű háromszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1976/szeptember: F.2052

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Jellemezzük először az olyan pontokat az $O_{1} O_{2}$ centrálisnak a két kör közé eső $L_{1} L_{2}$ szakaszán, amelyekre az állítás igaz.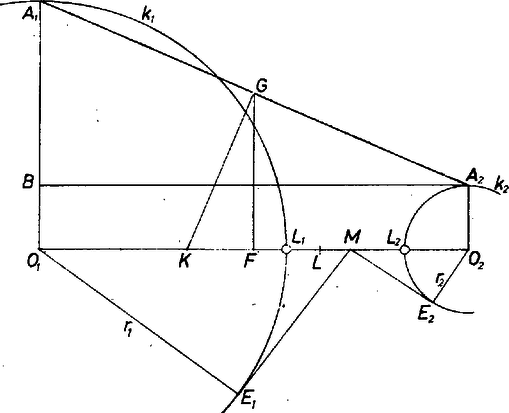

Miközben egy

M

pont

L_{1}

-től

L_{2}

-ig halad, a belőle a

k_{1}

és

k_{2}

körhöz húzott érintőnek a körig terjedő

M E_{1}

szakasza a szemlélet szerint nő, az

M E_{2}

szakasza pedig csökken. Valóban, négyzeteik különbsége

\begin{matrix} y = M E_{2}^{2} - M E_{1}^{2} = (M O_{2}^{2} - r_{2}^{2}) - (M O_{1}^{2} - r_{1}^{2}) = \\ (M O_{1} + O_{2} M) (M O_{2} - M O_{1}) + (r_{1}^{2} - r_{2}^{2}) = \\ O_{1} O_{2} (O_{1} O_{2} - 2 M O_{1}) + r_{1}^{2} - r_{2}^{2} = - 2 c \cdot O_{1} M + (c^{2} + r_{1}^{2} - r_{2}^{2}), \end{matrix}

ahol

c = O_{1} O_{2} (> r_{1} + r_{2})

, és ez

O_{1} M = x

növekedésével monoton csökken. Ha

x = r_{1}

, akkor

\begin{matrix} y = {(c - r_{1})}^{2} - r_{2}^{2} = O_{2} L_{1}^{2} - O_{2} L_{2}^{2} > 0, \end{matrix}

ha pedig

x = O_{1} L_{2} = c - r_{2}

, akkor

\begin{matrix} y = r_{1}^{2} - {(c - r_{2})}^{2} = O_{1} L_{1}^{2} - O_{1} L_{2}^{2} < 0, \end{matrix}

tehát az

y = 0

értéket adó egyetlen

L

pont az

L_{1} L_{2}

szakaszon van, és

\begin{matrix} O_{1} L = \frac{c^{2} + r_{1}^{2} - r_{2}^{2}}{2 c} = \frac{c}{2} + \frac{r_{1}^{2} - r_{2}^{2}}{2 c}, \end{matrix}

vagyis

L

a kisebbik kör középpontjához van közelebb, illetve éppen

O_{1} O_{2}

felezőpontjában van, ha

r_{1} = r_{2}

.
2. Számítsuk ki másrészt az

O_{2} K

szakasz hosszát. Ha ezt egyenlőnek találjuk

O_{1} L

-lel, akkor

K

és

L

O_{1} O_{2}

szakaszon szimmetrikusan helyezkednek el és ez bizonyítja az állítást. Választhatjuk úgy az indexeket, hogy

r_{1} \geq r_{2}

legyen, továbbá jelöljük

O_{1} O_{2}

és

A_{1} A_{2}

felezőpontját

F

-fel,

G

-vel,

A_{2}

-nek

O_{1} A

-n levő vetületét

B

-vel. Ekkor

K

O_{1} F

szakaszon van, vagy éppen

F

-ben, és a

K F G

A_{1} B A_{2}

derékszögű háromszögek hasonlósága alapján

\begin{matrix} F K = B A_{1} \cdot \frac{F G}{B A_{2}} = (r_{1} - r_{2}) \frac{r_{1} + r_{2}}{2 c} = \frac{r_{1}^{2} - r_{2}^{2}}{2 c}, \end{matrix}

hiszen

F G

O_{1} A_{1} A_{2} O_{2}

derékszögű trapéz középvonala. Így tüstént látjuk, hogy

O_{2} K = O_{2} F + F K

kifejezése egyezik

O_{1} L

fenti kifejezésével. Az állítást bebizonyítottuk.