I. megoldás. Az állítás ekvivalens azzal, hogy az $F$ fókuszt megadja az $M$ pont tükörképe a körök $O_1\mathrm{,}{O}_2$ középpontjait összekötő centrálisra nézve. Még máshogyan, hogy az $MF$ szakasz felező merőlegese átmegy $O_i$-n, $i=\mathrm{1,}2$. Ezt bizonyítjuk koordináta-geometriai úton, az $y=x^2$ normálparabola alapulvételével, hiszen minden parabola ennek nagyított vagy kicsinyített, eltolt, elfordított képe.
Legyen $T{}_i$ abszcisszája $u_i\left(u_2\ne u_1\ne 0\right)$. Az $y=x^2$ függvény $y\text{'}=2x$ deriváltja alapján $t_i$ egyenlete:

F(0;14),azMF szakasz felező merőlegese:

$\begin{array}{c}{\displaystyle \left(u_1+u_2\right)x+\left(2u_1{u}_2-\frac{1}{2}\right)y=u_1^2{u}_2^2+\left(\frac{u_1+u_2}{2}\right)-\frac{1}{16}\mathrm{.}}\end{array}$

(1)

A behelyettesítés mutatja, hogy $O_2$ rajta van ezen az egyenesen. Ezzel az előrebocsátottak szerint állításunkat $O_2$-re bebizonyítottuk.
$O_1$-et $O_2$ ből az $1$ és $2$ indexek fölcserélésével kaphatnánk, hiszen $O_1$ meghatározásában $t_1$ helyére $t_2$ lép és $T_2$ helyére $T_1$, de $O_1$ koordinátáinak (1)-be való bepróbálása mellőzhető. Ugyanis azt az egyenletet mindenesetre kielégítenék, amely (1)-ből keletkezik az indexcserével, viszont ez a csere (1)-et önmagába viszi át. Eszerint (1)-et $O_1$ is kielégíti. ‐ A bizonyítást befejeztük.

 

II. megoldás. Az $F$ fókusz akkor és csak akkor van rajta $k_1$-en, ha az $\alpha \text{'}=T_{2}MF\sphericalangle$, ami az $F$ illeszkedésétől függetlenül is (érintő szárú) kerületi szög a $k_1$-re nézve, egyenlő az $M{T}_{1}F\sphericalangle =\alpha$-val. Ugyanígy $k_2$ akkor és csak akkor megy át $F$-en, ha a $\beta \text{'}=T_{1}MF\sphericalangle \text{és a}\beta =M{T}_{2}F\sphericalangle$-ek egyenlőek. Ezt a két szögegyenlőséget bizonyítjuk.
Legyen $T_i$ vetülete a parabola vezéregyenesén $T{\text{'}}_i$. Ismeretes, hogy $t_i$ felezi a $T_{i}F$ és $T_{i}T{\text{'}}_i$ félegyenesek közti szöget, másrészt a parabola definíciója alapján $T_{i}F=T_{i}T{\text{'}}_t$. Ezekből következik, hogy $T_i$ és $F$ egymás tükörképei $t_i$-re, tehát $M$-re mint a szimmetriatengely pontjára egyrészt $T{\text{'}}_{1}M=FM$, tehát $T{\text{'}}_{1}M=T{\text{'}}_{2}M$, másrészt $T_{2}MT{\text{'}}_2\sphericalangle =\alpha \text{'}$, és $T_{1}MT{\text{'}}_1\sphericalangle =\beta \text{'}$; továbbá, hogy $M{T}_{1}T{\text{'}}_1\sphericalangle =\alpha$ és $M{T}_{2}T{\text{'}}_2\sphericalangle =\beta$.
Az $MT{\text{'}}_{1}T{\text{'}}_2$ egyenlő szárú háromszög tengelye párhuzamos $T_{i}T{\text{'}}_i;$-vel, ezért $MT{\text{'}}_1{T}_1\sphericalangle =MT{\text{'}}_2{T}_2\sphericalangle$, és az $MT{\text{'}}_1{T}_1\mathrm{,}MT{\text{'}}_2{T}_2$ háromszögekből $\alpha +\beta \text{'}=\alpha \text{'}+\beta$.
Másrészt a $T_{1}M{T}_2\sphericalangle =\alpha \text{'}+\beta \text{'}$ szöget kifejezhetjük $\alpha$-val és $\beta$-val.

 

 

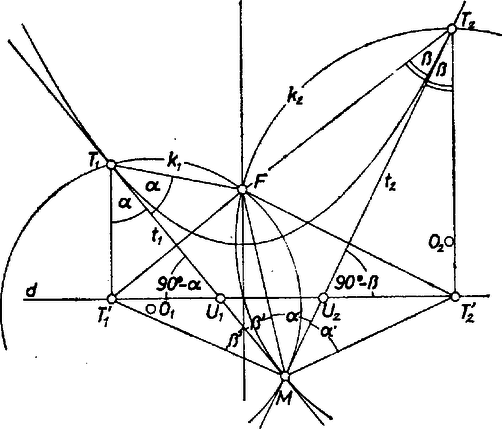1. ábra

 

Legyen $t_i$ metszéspontja $d$-vel $U_i$, ekkor a $T_{1}M{T}_2\sphericalangle$ egyenő az $U_{1}M{U}_2\sphericalangle$-gel (1. ábra), illetve egymás mellékszögei (2. ábra), de mindkét esetben csekély további számítás szerint $\alpha +\beta$ az értéke, tehát $\alpha \text{'}+\beta \text{'}=\alpha +\beta$.

 

 

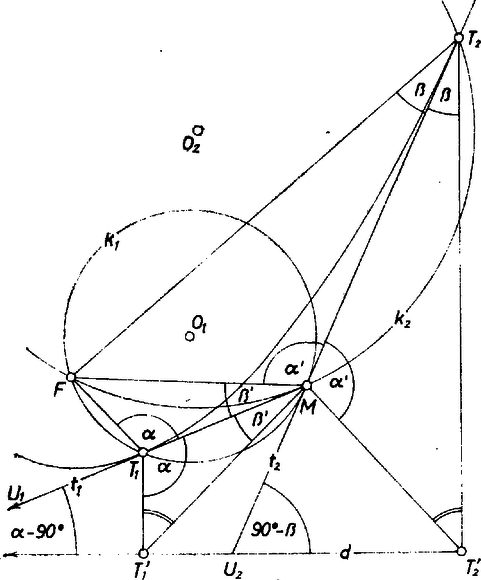2. ábra

 

Ezt az előbbi egyenletből kivonva $\alpha -\alpha \text{'}=\alpha \text{'}-\alpha$, tehát $\alpha \text{'}=\alpha$, majd tovább $\beta \text{'}=\beta$. Ezeket akartuk bizonyítani.
$U_1$ és $U_2$ közül legföljebb az egyik nem jön létre, pl. $U_1$ nem, ha $T_1$ éppen a parabola csúcsa, és akkor $\alpha ={90}^{\circ }$. Ekkor közvetlenül látjuk a $T_{1}M{T}_2\sphericalangle ={90}^{\circ }+\beta =\alpha +\beta$ egyenlőséget. ‐ Ugyanezt kapjuk akkor is, ha $M$ éppen a $d$-n adódik.

 

  Váradi Ferenc (Miskolc, Földes F. Gimn., III. o. t.)

 

Megjegyzések. 1. Mindkét megoldásból kiolvasható, hogy az $M$-et a $T_1{T}_2$ húr felezőpontjával összekötő egyenes merőleges $d$-re, tehát megadja a parabola tengelyének irányát. Ez is érdekes, egyszerű tulajdonsága a parabola két érintőjének.
2. Ha a feladat állítását mint $F$ megszerkesztésének lehetőségét tekintjük a $T_1\mathrm{,}{T}_2\mathrm{,}M$ ponthármasból, akkor kiolvasható az a megfordítása is, ha adott $F\mathrm{,}{t}_1$ és $t_2$ (a $T_1\mathrm{,}{T}_2$ nélkül), tehát $M$ is: vesszük $F$ tükörképeit $t_i$-re, ezekből $T{\text{'}}_{1}T{\text{'}}_2$ a vezéregyenes, és az erre $T{\text{'}}_i$-ben emelt merőleges $t_i$-ből kimetszi a $T_i$ érintési pontot.
3. Az állításnak az a fele, hogy bármelyik $k_i\left(i=\mathrm{1,}2\right)$ átmegy $F$-en, speciális esete Lambert tételének, ^{${}^{*}$}, amely szerint a parabola 3 érintője által meghatározott háromszög körülírt köre átmegy a fókuszon. Ugyanis pl. $t_1$-en $T_1$ megadása azt jelenti, hogy $t_1$ és $T_1$ határátmenettel kétszeresen használható fel: $t_1$ és $t_1$ ,,metszéspontja'' $T_1$, ,,azokat'' $t_2$ ,,$M$-ben és $M$-ben'' metszi, és így a $T_{1}MM$ ,,háromszög'' köré írt $k_1$ kör az $M$ (és $M$) pont(ok)-ban érinti $t_2$-t.

---

^{${}^{*}$}Lásd pl.: Dörrie, H.: A diadalmas matematika (Gondolat Kiadó, Budapest, 1965) 224. old.