Kezdőlap


Feladat:	F.2040	Korcsoport: 18-	Nehézségi fok: -
Füzet:	1976/november, 130 - 131. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Beírt kör, Sokszögek súlypontjának koordinátái, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1976/április: F.2040

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $A B C$ háromszögben az $α : β : γ = 1 : 3 : 4$ arányok alapján $γ$ derékszög, tegyük ennek alapján $C$ -t a koordináta-rendszer origójába és $A$ -t az $x$ tengely ( $b, 0$ ) pontjába ( $b > 0$ ). Ekkor $B$ az $y$ tengelyre jut, válasszuk helyzetének a ( $0, a$ ) pontot ( $a > 0$ ), végül legyen $A B = 1$ , azaz $a^{2} + b^{2} = 1$ .
A beírt kör sugara, mint ismeretes:

\begin{matrix} ϱ = \frac{1}{2} (a + b - c) = \frac{1}{2} (a + b - 1), \end{matrix}

evvel

K

középpontja a (

ϱ, ϱ

) pont; az

S

súlypont pedig

(\frac{b}{3}, \frac{a}{3})

. Ennélfogva

S

akkor esik rá a

K

körüli sugarú kör kerületére, ha

\begin{matrix} {(\frac{b}{3} - ϱ)}^{2} + {(\frac{a}{3} - ϱ)}^{2} = K S^{2} = ϱ^{2}, \end{matrix}

és

ϱ

kiküszöbölésével

\begin{matrix} 16 - 3 {(a + b + 1)}^{2} = 0, \end{matrix}

amiből

\begin{matrix} a + b = \frac{4}{\sqrt[]{3}} - 1. \end{matrix}

(1)

Másrészt a feltételből

α = 45^{\circ} / 2, β = 90^{\circ} - α

, és ismert összefüggések alapján

\begin{matrix} a + b = sin α + sin (90^{\circ} - α) = 2 sin 45^{\circ} cos (45^{\circ} - α) = \sqrt[]{2} cos {22, 5}^{\circ} = \sqrt[]{2} \sqrt[]{\frac{1 + cos 45^{\circ}}{2}} = \sqrt[]{1 + \frac{1}{\sqrt[]{2}}} . & (2) \end{matrix}

Az (1) és (2) kifejezések nem lehetnek egyenlők. Ugyanis különbségüket az összegükkel szorozva, ami biztosan pozitív,

\begin{matrix} \frac{16}{3} - (\frac{8}{\sqrt[]{3}} + \frac{1}{\sqrt[]{2}}) \end{matrix}

adódik, és ez nem

0

, mert hasonlóan

\begin{matrix} [\frac{16}{3} - (\frac{8}{\sqrt[]{3}} + \frac{1}{\sqrt[]{2}})] \cdot [\frac{16}{3} + (\frac{8}{\sqrt[]{3}} + \frac{1}{\sqrt[]{2}})] = \frac{256}{9} - (\frac{131}{6} + \frac{16}{\sqrt[]{6}}) = \frac{119}{18} - \frac{16}{\sqrt[]{6}} \end{matrix}

sem

0

, különben ugyanis

\sqrt[]{6} = 16 \cdot 18 / 119

, racionális szám lenne.
Ezek szerint a szögek fenti aránya, és a beírt körnek a súlyponton való áthaladása ugyanazon derékszögű háromszögben nem teljesülhet, a kérdéses állítás nem igaz.

Megjegyzések. 1. Kérdezhetjük : mennyire ,,jár közel'' egymáshoz a két feltétel ? (1) és (2) egyemlősége egyenletet ad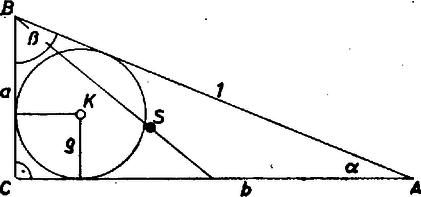

α

-ra:

\begin{matrix} cos (45^{\circ} - α) = \frac{4 - \sqrt[]{3}}{\sqrt[]{6}} = \frac{4 \sqrt[]{6} - 3 \sqrt[]{2}}{6} = 0, 9259, \end{matrix}

α = 22^{\circ} 48'

, vagyis kb.

0, 3^{\circ}

az eltérése

22, 5^{\circ}

-tól.

2. A lapunk 32. kötetének (1966) 220. oldalán hirdetett pályázat összefüggést keresett a háromszög oldalai között, ha a súlypont rajta van a beírt kör kerületén. Ez:

6 (a b + b c + c a) - 5 (a^{2} + b^{2} + c^{2}) = 0

, átrendezéssel:

3 {(a + b)}^{2} + 6 (a + b) c - 8 (a^{2} + b^{2}) - 5 c^{2} = 0

, ebből is kiadódik az (1) egyenlet.