|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldás. Ismeretes, hogy ilyen mozgást végző test út‐idő függvénye másodfokú polinom a szokásos jelölésekkel . A kérdés tehát az, hogy másodfokú polinom helyettesítési értékeivel mennyire tudjuk megközelíteni a táblázat adatait.
Ha a táblázat út‐adataiból kivonjuk egy tetszőleges másodfokú polinom értékeit, a kapott új táblázat adatait ugyanannyira lehet megközelíteni egy polinommal, mint az eredetit a -vel.
Olyan polinomot szeretnénk találni, amelyet a táblázat értékeiből kivonva, a kapott új táblázat ,,szebb'' lesz, könnyebben felismerhető lesz a jól közelítő polinom. Táblázatunkat nézegetve észrevehető, hogy a s-hoz tartozó adat az s-hoz tartozó -szeresénél -gyel nagyobb, | |
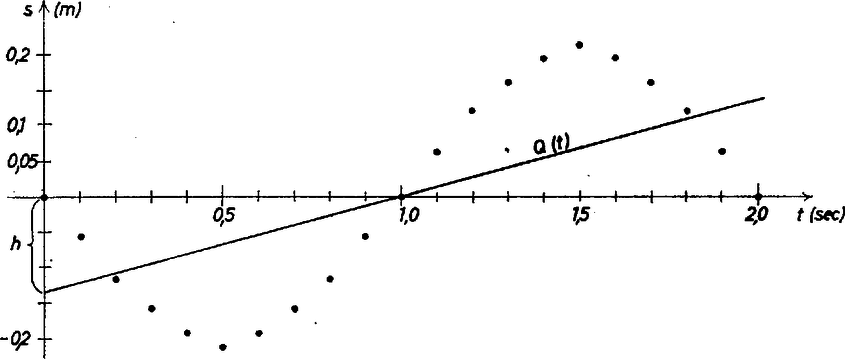
az idő négyzetének felét levonva belőlük, éppen -szerese lesz annak (, ill. ). Vonjuk le ezért a táblázatból a polinomot. A kapott különbségeket az új táblázat tartalmazza, ábrázoljuk is a pontokat koordináta‐rendszerben. A kapott pontrendszer lényegében szimmetrikus az pontra pontnál van eltérés), ezért jól közelíthető egy, a szimmetriaközépponton áthaladó egyenessel. Az egyenes iránytangensét úgy határozzuk meg, hogy a és a pontokban azonos legyen a hiba (könnyen belátható, hogy ezen két pont esetén adódik a hiba a legnagyobbnak). A hibát -val jelölve, hasonló háromszögekből felírható, hogy
amiből adódik. Tehát az egyenes egyenlete , a mozgást közelítően leíró függvény és a hiba minden pontban kisebb, mint .
Alsó becslést kapunk a hibára, ha csak a és abszcisszájú pontokhoz akarunk legjobban közelítő másodfokú függvényt találni. Ezen számokhoz (és általában tetszőleges ilyen szám‐négyeshez) meghatározhatók a számok úgy, hogy teljesüljenek a egyenlőségek. Ez három egyenlet a ismeretlenekre. Bebizonyítható, hogy az egyenletrendszernek mindig van (végtelen sok) megoldása. Esetünkben egy megoldás (a számolást nem részletezzük). Jelöljük -vel a -ben mért értéket, és legyen , a helyen a közelítés hibája. Ekkor | | (2) |
(2)-ben az utolsó egyenlőség jobb oldalán álló 3 kivonandó tag (1) szerint , tehát Mindkét oldal abszolút értékét véve, és felhasználva, hogy az összeg abszolút értéke nem nagyobb a tagok abszolút értékeinek összegénél, | |
amiből kapjuk, hogy | | (3) |
A (3) képletet a kiválasztott pontnégyesre és a már meghatározott -kre alkalmazva nyerjük, hogy Nyilvánvaló, hogy a teljes pontrendszert közelítő parabola hibája ennél csak nagyobb lehet. Viszont hibával közelítő parabolát már találtunk, tehát kimondhatjuk, hogy az út mérési hibája legalább egység. (Nincs értelme a -hoz keresni parabolát ‐ habár találnánk ilyet ‐, hiszen az eredeti adatok is csak 3 tizedes pontosságúak voltak.)
|
 PDF |
PDF |  MathML
MathML