Kezdőlap


Feladat:	F.2017	Korcsoport: 16-17	Nehézségi fok: -
Füzet:	1976/április, 159 - 161. oldal		PDF \| MathML
Témakör(ök):	Magasságpont, Körülírt kör középpontja, Síkgeometriai szerkesztések, Ellipszis, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1975/december: F.2017

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Mivel a háromszög hegyesszögű, mind $O$ , mind $M$ a háromszög belsejében van.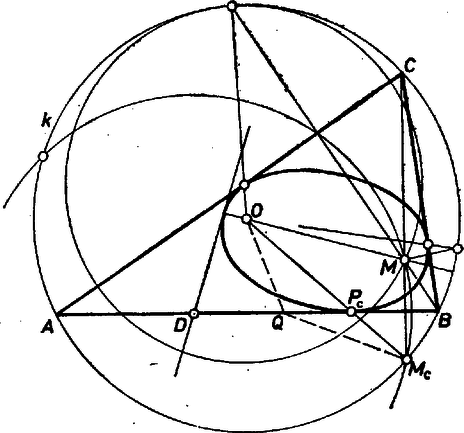
Tudjuk, hogy a háromszög magasságpontját bármely oldalára tükrözzük, a tükörkép rajta lesz a háromszög köré írható körön. Tükrözzük $M$ -et $A B$ -re, jelöljük tükörképét $M_{c}$ -vel, az $M_{c} O$ szakasznak $A B$ -vel közös pontját $P_{c}$ -vel (mivel a háromszög hegyesszögű, van ilyen pont). A tükrözés miatt $M P_{c} = M_{c} P_{c}$ , $O P_{c}, + P_{c} M = O P_{c} + P_{c} M_{c} = O M_{c} = r$ az ellipszis nagytengelye, azaz $P_{c}$ rajta van az $O$ , $M$ fókuszú $O M_{c} = r$ hosszúságú nagytengelyű ellipszisen.

Belátjuk, hogy az

A B

egyenesnek több ilyen tulajdonságú pontja nincs. Legyen

Q

tetszőleges,

A B

-re illeszkedő,

P_{c}

-től különböző pont. Mivel

M_{c}

M

tükörképe

A B

-re, ezért

M_{c} Q = M Q

, így

O Q + Q M = O Q + Q M_{c}

. Tekintsük az

O M_{c} Q

háromszöget! A háromszög-egyenlőtlenség miatt

O Q + Q M_{c} > O M_{c} = r

, így

Q

nem pontja az ellipszisnek. Mivel

P_{c}

belső pontja

A B

-nek, ezért

A B

szakasznak egyetlen közös pontja van az ellipszissel, így azt is mondhatjuk, hogy

A B

érintő. Az

A B

tetszőleges oldala volt a háromszögnek, ezért az állítást mindhárom oldalra beláttuk.

Megjegyzések. 1. A látott tulajdonság alapján szinte nyilvánvaló, hogy a tekintetbe vett ellipszis adja azon körök középpontjának mértani helyét, amelyek átmennek az (

A B C

háromszög köré írt

k

körben levő)

M

ponton és (belülről) érintik

k

-t. Az ellipszisnek ilyen felfogása alkalmat ad számos szerkesztésre. Itt az

O

és

M

fókuszok egyenrangúsága nem érvényesül, ezért szokás más neveket használni: a

k

kör az ún. ellenkör (sugara a nagytengely),

O

az ellenkör középpontja és

M

"a'' fókusz. (Természetesen lehetne

M

körül is felvenni ellenkört, a két ellenkör egyidejű felhasználása viszont nem ígér előnyt.)
Csak egy efféle szerkesztési példát említünk (elfogadva a fentiekből, hogy az

A B

egyenes az ellipszisnek

P_{c}

-beli érintőjével azonos): húzzuk meg az érintőket az ellipszishez az

A B

egyenes tetszőleges (

A

-tól,

B

-től és

P_{c}

-től különböző)

D

pontjából. A fentiekből

D M_{c} = D M

, tehát a

D

körüli

M

-en (a fókuszon) átmenő kör az ellenkörből kimetszi a

(P_{c})

érintési pontot tartalmazó

O M_{c}

ellenköri sugár

M_{c}

végpontját, így a keresett (egyik) érintő az

M M_{c}

szakasz felező merőlegese. ‐ Az olvasóra hagyjuk annak vizsgálatát, milyen helyzetű

D

-hez adódik

2

, ill.

1

érintő, és hogy milyen

D

-hez nem kapunk

M_{c}

-t, érintőt.
Az érdeklődőknek ajánljuk a következő szakköri füzetet: Schopp János: Kúpszeletek (Tankönyvkiadó, Budapest, 1965.)
3. Az eddigieket folytatva, eredeti feladatunk egyértelmű a következő tétellel: az ellipszis bármely érintője

2

pontban metszi az ellenkört (fent

A

és

B

). Megrajzolva e pontokból az ellipszis második érintőit, ezek

(C)

metszéspontja rajta van az ellenkörön. (Szokásos kifejezéssel: a három érintő záródik, az eljárást folytatva további új érintőt nem kapunk.) Ez a tétel Schopp Jánostól (Budapest) származik.