Kezdőlap


Feladat:	F.2016	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Balázs I. , Becze I. , Benyák Gabriella , Bodó Z. , Brindza B. , Csapó I. , Csikós B. , Futó I. , Gáti T. , Gulyás M. , Homonnay G. , Honos A. , Horváth 712 I. , Husvéti T. , Kirch Z. , Kiss 311 B. , Knébel I. , Kőrösi G. , Kramarics G. , Krenedits S. , Lacskó M. , Láng Zs. , Lévai L. , Lugosi E. , Márkus G. , Miklós D. , Nagy L. , Neumüller I. , Nőthig L. , Novák Z. , Pap 224 L. , Posgay Gy. , Pyber L. , Pörneczi T. , Rapai G. , Révész Sz. Gy. , Soukup L. , Specker N. , Spissich L. , Surány G. , Szalay 195 S. , Szalontai S. , Szőke R. , Tankovits T. , Tóth Csaba , Wolf Gy. , Zimmer Zsuzsanna
Füzet:	1976/április, 158 - 159. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Derékszögű háromszögek geometriája, Indirekt bizonyítási mód, Feladat
Hivatkozás(ok):	Feladatok: 1975/december: F.2016

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Bármelyik tekintett harmadoló egyenes a háromszög belsejében metszi a másik két csúcsból induló két-két harmadolót. Így egy kiszemelt csúcsból induló két harmadolón $2 \cdot 2 \cdot 2 = 8$ metszéspontot találunk ‐ hacsak ezek mind különbözők. Mind a három csúcsból külön-külön kiindulva, így $3 \cdot 8$ metszéspontot számlálunk, de ezzel mindegyiket $2$ -szer vettük tekintetbe, tehát a pontok száma legfeljebb 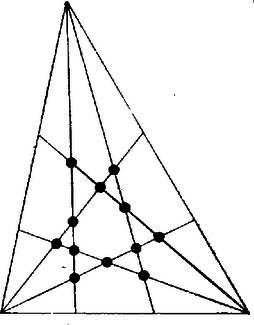$12$ .

Bebizonyítjuk, hogy minden háromszögben létre is jön ez a

12

metszéspont. Elég ehhez tekinteni az

A B C

háromszög

A A_{1}

szögharmadolójából

(C A A_{1} ∢ = 2 \cdot B A A_{1} ∢)

B B_{1}

és

B B_{2}

harmadolókkal

(A B B_{1} ∢ = 2 \cdot C B B_{1} ∢

C B B_{2} ∢ = 2 \cdot A B B_{2} ∢)

kimetszett

M_{1}

M_{2}

metszéspontokat, és megmutatni, hogy sem

M_{1} C

, sem

M_{2} C

nem harmadolja az

A C B

szöget hiszen a csúcsok kellő átbetűzésével ez a bizonyítás minden metszéspontra átvihető.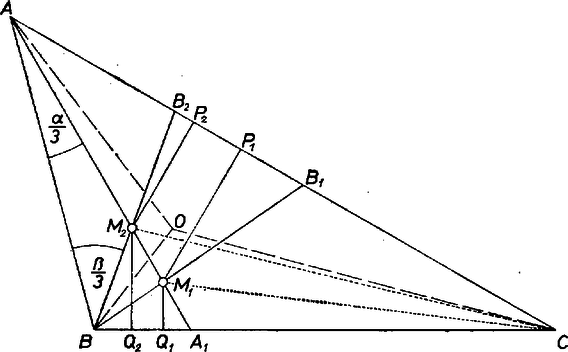

Jelöljük az

A B M_{i}

háromszög köré írt kör átmérőjét

d_{i}

-vel,

M_{i}

-nek

A C

-n,

B C

-n levő vetületét

P_{i}

-vel,

Q_{i}

-vel

(i = 1, 2)

. Ekkor

\begin{matrix} \frac{M_{1} P_{1}}{M_{1} Q_{1}} = \frac{A M_{1} sin \frac{2 α}{3}}{B M_{1} sin \frac{β}{3}} = \frac{d_{1} sin \frac{2 β}{3} sin \frac{2 α}{3}}{d_{1} sin \frac{α}{3} sin \frac{β}{3}} = 4 cos \frac{α}{3} cos \frac{β}{3} . \end{matrix}

M_{1} C

harmadolná a

C

-nél levő

γ

szöget, ez csak úgy lehetne, hogy

A C M_{1} ∢ = 2 \cdot B C M_{1} ∢

mert ‐ a szögfelezők közös pontját

O

-val jelölve ‐

M_{1}

O B C

háromszögben van, hiszen

A A_{1}

B A O

B B_{1}

pedig a

C B O

szögtartományban halad. Feltéve tehát, hogy

B C M_{1} ∢ = \frac{γ}{3}

\begin{matrix} \frac{M_{1} P_{1}}{M_{1} Q_{1}} = \frac{C M_{1} sin \frac{2 γ}{3}}{C M_{1} sin \frac{γ}{3}} = 2 cos \frac{γ}{3} = 4 cos \frac{α}{3} cos \frac{β}{3} \end{matrix}

lenne, vagyis

\begin{matrix} cos \frac{γ}{3} = 2 cos \frac{α}{3} cos \frac{β}{3} . \end{matrix}

(1)

Ez azonban nem állhat fenn, a jobb oldal mindig nagyobb a bal oldalnál, ugyanis így alakítható:

\begin{matrix} cos \frac{α - β}{3} + & cos \frac{α + β}{3} = cos \frac{α - β}{3} + cos (60^{\circ} - \frac{γ}{3}) = \\ cos \frac{α - β}{3} + \frac{1}{2} cos \frac{γ}{3} + \frac{\sqrt[]{3}}{2} sin \frac{γ}{3} = \\ cos \frac{γ}{3} + [cos \frac{α - β}{3} - cos (60^{\circ} + \frac{γ}{3})], \end{matrix}

és itt a nagy zárójel pozitív, hiszen a cosinusfüggvény a

(0^{\circ}, 180^{\circ})

intervallumban szigorúan monoton fogyó és

\begin{matrix} 0^{\circ} ≦ | \frac{α - β}{3} | < 60^{\circ} < 60^{\circ} + \frac{γ}{3} < 180^{\circ} . \end{matrix}

Hasonló számítással

\begin{matrix} \frac{M_{2} P_{2}}{M_{2} Q_{2}} = \frac{sin \frac{β}{3} sin \frac{2 α}{3}}{sin \frac{α}{3} sin \frac{2 β}{3}} = \frac{cos \frac{α}{3}}{cos \frac{β}{3}}, \end{matrix}

és ennek ‐ ha

M_{2} C

harmadolná

γ

-t ‐ ismét vagy

2 cos \frac{γ}{3}

-mal vagy ennek reciprokával kellene egyenlőnek lennie ‐ és mindkét föltevés alkalmas átbetűzéssel (1)-re vezetne.
Ezzel az állítást bebizonyítottuk.