Kezdőlap


Feladat:	F.2007	Korcsoport: 16-17	Nehézségi fok: -
Megoldó(k):	Bodó Z. , Csapó Ildikó , Cseke I. , Csikós B. , Gál 327 L. , Hőbenreich L. , Holop L. , Homonnay G. , Kirch L. , Kiss 311 B. , Knébel I. , Koltay K. , Krenedits S. , Köteles Z. , Láng Zs. , Magyar Z. , Nagy 264 I. , Németh V. , Pörneczi T. , Sali A. , Soukup L. , Szigeti A. , Szőke R. , Torma József , Tuba Csilla , Vándor T. , Vindics J. , Wolf Gy.
Füzet:	1976/március, 100 - 103. oldal		PDF \| MathML
Témakör(ök):	Sakk, Kombinatorikai leszámolási problémák, Négyzetrács geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1975/november: F.2007

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A könnyebb kezelhetőség céljából a végtelen sakktábla mezőit a mezők középpontjaival képviseltetjük. Ezen középpontoknak egy síkbeli derékszögű koordináta‐renszerben azokat a pontokat tekintjük, amelyeknek mindkét koordinátája egész szám. A huszár induljon az origóból.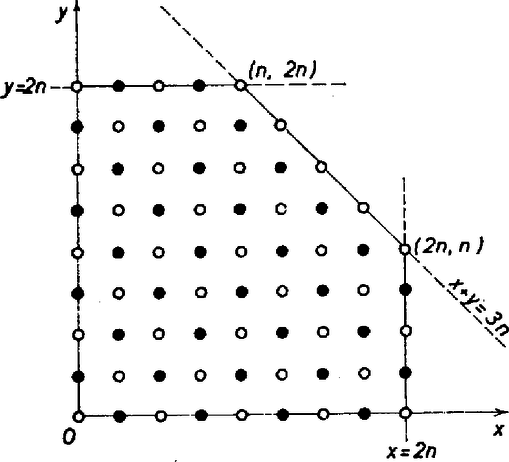
A sakktáblán sötét és világos mezők váltogatják egymást. Megállapíthatjuk, hogy mindazok a rácspontok, amelyek koordinátáinak összege páros, ugyanolyan színű mezőket képviselnek, mint az origó. Azok a rácspontok pedig, amelyek koordinátáinak összege páratlan, az origóval ellenkező színű mezőknek felelnek meg.
Mivel a huszár minden lépésekor a rácspont egyik koordinátájának paritása változatlan marad, a másiké pedig megváltozik, az elért rácspont színe minden lépésnél megváltozik. Ebből következik, hogy a huszár páros számú lépéssel csak az origó színével egyező színű rácspontokra érkezhet, páratlan számú lépéssel pedig csak az ellenkező színűekre.
Valamely adott számú lépés után elérhető rácspontok közös színét az adott számú lépés esetén a továbbiakban "megfelelő szín''-nek nevezzük.
A következőkben először is azt vizsgáljuk, hogy hol húzódik az a határ, amelyet az $n$ -edik lépésben a huszár elérhet, de nem léphet túl. Ezt elég az első síknegyedben megállapítani, mivel a négy síknegyed teljesen egyenrangú.
Az $n$ lépéssel elérhető szélső pontokban $x$ legfeljebb $2 n$ lehet, $y$ szintén $2 n$ , Ugyanakkor azonban $x + y$ legfeljebb $3 n$ lehet, mivel a két koordináta összege minden lépésben legfeljebb 3-mal növekedhet.
Az első síknegyednek azokat a rácspontjait, amelyek mindhárom feltételnek eleget tesznek, az 1. ábrán látható tartomány (a határát is beleértve) tartalmazza.

1. ábra

A tartományt a tengelyekre és az origóra tükrözve olyan nyolcszög adódik, amelyen kívüli rácspontokba

n

(vagy

n

-nél kevesebb) lépéssel nem juthatunk (2. ábra). Jelöljük ezt a nyolcszöget

T_{n}

-n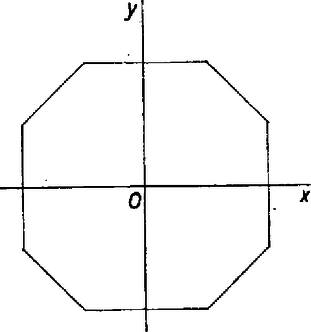el.

2. ábra

Nevezzük

T_{n}

-t telítettnek, ha a huszár az

n

-edik lépésben

T_{n}

minden megfelelő színű rácspontjába megérkezhet.
Közvetlenül éllenőrizhető, hogy

T_{1}

és

T_{2}

nem telített,

T_{3}

viszont igen (3. ábra).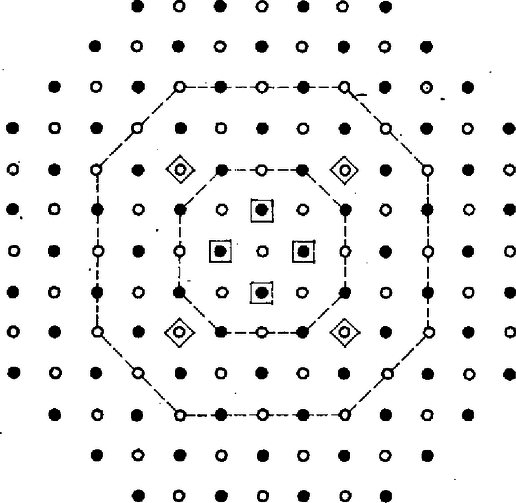

3. ábra

T_{1}

-ben és

T_{2}

-ben is 4 olyan megfelelő színű rácspontot találunk, amelyek 1 ill. 2 lépéssel nem érhetők el (bekeretezett sötét ill. világos pontok).
A teljes indukció módszerével bebizonyítjuk, hogy

T_{n}

minden

n \geq 3

esetén telített. Mivel

T_{3}

-ról már tudjuk, hogy telített, azt kell még bebizonyítanunk, hogy ha

T_{n}

telített, akkor

T_{n + 1}

is az. Ehhez azt bizonyítjuk, hogy ha

T_{n + 1}

nem telített, akkor

T_{n}

sem telített.
Ha van olyan megfelelő színű rácspont

T_{n + 1}

-ben, amelyre a huszár az

(n + 1)

-edik lépésben nem érkezhet meg, akkor nyilván nem lehet ettől lóugrásnyira olyan rácspont, amelyre az

n

-edik lépésben megérkezhet. Viszont a

T_{n + 1}

-ben levő bármely rácsponttól lóugrásnyira fekvő rácspontok között mindig van legalább egy, amely

T_{n}

-ben is benne van (4. ábra).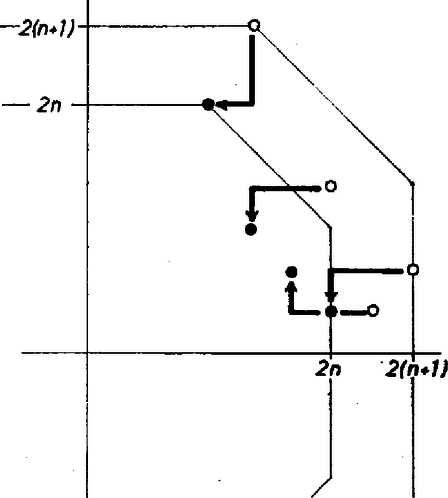

4. ábra

Akkor a

T_{n + 1}

-ben megfelelő színű rácspontoktól lóugrásnyira fekvő rácspontok között is van ilyen, s ez

T_{n}

-ben megfelelő színű. Tehát

T_{n}

nem telített. Azaz a telítettség

T_{n}

-ről

T_{n + 1}

-re öröklődik,

T_{n}

valóban minden

n \geq 3

esetén telített.
Most már csak össze kell számolnunk

T_{n}

-ben a megfelelő színű rácspontokat (5. ábra).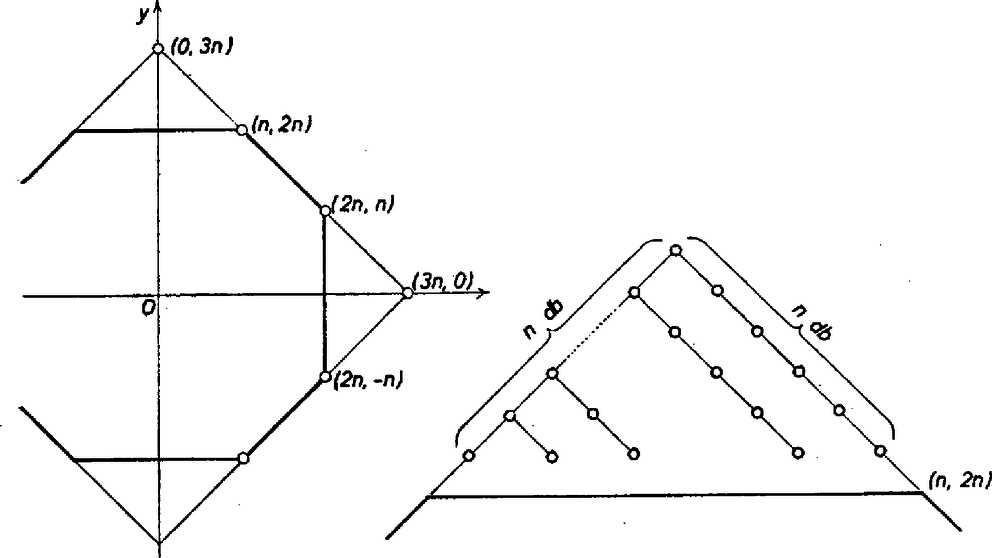

5. ábra

A nyolcszög oldalai csupa megfelelő színű rácspontot tartalmaznak. Az átlós oldalak egyenesei egy négyzetet zárnak közre, amelynek minden oldalán

(3 n + 1)

darab megfelelő színű rácspont található. Ezért ez a négyzet

{(3 n + 1)}^{2}

darab megfelelő színű rácspontot tartalmaz. A

T_{n}

tartomány ennél

(4 \sum_{i = 1}^{n} i)

-vel kevesebbet, hiszen mind a négy levágott sarokban egyaránt

\sum_{i = 1}^{n} i

darab megfelelő színű rácspont van.
Végeredményben az

n

-edik lépésben elérhető rácspontok (mezők) száma

\begin{matrix} L_{n} = {(3 n + 1)}^{2} - 4 \frac{1 + n}{2} \cdot n = 7 n^{2} + 4 n + 1, ha n \geq 3; \end{matrix}

n = 1

és

n = 2

esetén pedig a képlet által megadott számnál 4-gyel kevesebb, vagyis

L_{1} = 8

és

L_{2} = 33

Torma József (Budapest, Apáctai Csere J. Gyak. Gimn., III. o. t.)

Megjegyzések. 1. A végtelen sakktáblán az egyik mezőről a másik mezőre vezető lehető legkevesebb lóugrás számát nevezhetjük a két pont távolságának. Hogy milyen alapon nevezhetjük az így definiált mennyiséget távolságnak és milyen ezen a síkon egy egyenes, az kiderül Kárteszi Ferenc: Egy különös geometria c. cikkéből (KÖMAL 9. kötet (1954) 71‐78. o.). A cikkhez kapcsolódott 644. és 652. feladatunk (szintén a 9. kötetben, megoldásuk a 10., ill. 11. kötetben jelent meg). Az utóbbi mostani feladatunkhoz igen hasonló kérdést vizsgált. A feladat szövege ez volt: A végtelen sakktábla kijelölt mezejéhez hány olyan mező tartozik, amely

n

lóugrással érhető el ‐ de annál kevesebbel már nem ?
2. Többen helyesen adták meg az elérhető mezők számát, de nem bizonyították, hogy azok az

n

-edik lépésben el is érhetők. Mások a mezők megszámolásánál hibáztak. Megint mások ‐ félreértve a feladatot ‐ lényegében a 652. feladat kérdésére válaszoltak.
3. A feladat

n

helyett

2 n

-nel megoldásával együtt megtalálható N. J. Vilenkin: Kombinatorika c. könyvében (374. feladat, 244. old.).