Feladat:	F.2004	Korcsoport: 16-17	Nehézségi fok: -
Megoldó(k):	Bodó Z. ,  Brindza Béla ,  Gulyás M. ,  Homonnay G. ,  Husvéti T. ,  Krenedits S. ,  Magyar Z. ,  Nagy 578 I. ,  Tornóci L. ,  Vindics J.
Füzet:	1976/február, 63 - 67. oldal		PDF  |  MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Körülírt kör, Beírt kör, Lefedések, Síkgeometriai számítások trigonometria nélkül körökben, Síkgeometriai számítások trigonometriával, Sokszögek szimmetriái, Feladat
Hivatkozás(ok):	Feladatok: 1975/október: F.2004

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 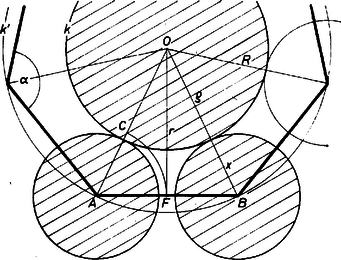$\begin{array}{c}{\displaystyle R-\frac{a}{2}\le \varrho \le r\mathrm{,}}\end{array}$ (1) 1. Legyen a szabályos $n$-szög középpontja $O$, egy oldala $AB$, ennek felezőpontja $F$, és mérjük fel $A$-tól $O$ felé az $AC=AF$ hosszúságot (1. ábra).     1. ábra   A háromszög‐egyenlőtlenség alapján az $OAF$ derékszögű háromszögből $\begin{array}{c}{\displaystyle OC=OA-AF<OF\mathrm{,}R-\frac{a}{2}<r\mathrm{,}}\end{array}$ eszerint $\varrho$-nak (1)-beli korlátai valóban egy intervallumot engednek meg $\varrho$ megválasztására. Az $O$ körül irandó $k$ körnek vagy át kell mennie $C$-n vagy magába kell zárnia $C$-t; viszont $\varrho \le r$ miatt $F$ legföljebb $k$ kerületéhez tartozhat hozzá, így $k$ egész belseje részt vesz a vizsgálandó lefedésben. Az $n$ szög csúcsai körül irandó $n$ számú kör mindegyikének sugara $R-\varrho$, jelöljük ezt $x$-szel, és jellemezzük ezzel a lefedést, tehát $\varrho =R-x$. (1)-et $\left(-1\right)$-gyel szorozva és mind a három részéhez $R$-et hozzáadva teljesülnie kell az $\begin{array}{c}{\displaystyle \frac{a}{2}\geqq R-\varrho =x\geqq R-r}\end{array}$ (2) kettős egyenlőtlenségnek. Az első rész szerint bármelyik két ilyen kör nem nyúlhat egymásba, hiszen két középpont távolsága legalább akkora, mint $AB=a$, ami legalább akkora, mint $2x$. Az $x$ sugarú körök a szabályos $n$-szög területéből egy‐egy $\alpha$ nyílásszögű körcikket fednek le, ahol $\alpha$ a szabályos $n$ szög egy szöge, ívmértékben $\begin{array}{c}{\displaystyle \frac{\left(n-2\right)\pi }{n}=\pi -\frac{2\pi }{n}\mathrm{.}}\end{array}$ Így a lefedett terület $\begin{array}{c}{\displaystyle T=\pi {\left(R-x\right)}^2+n\frac{x^2}{2}\left(\pi -\frac{2\pi }{n}\right)\mathrm{,}}\end{array}$ és ennek ugyanazon $x$ (és megfelelő $\varrho$) mellett van maximuma, illetve minimuma, mint a (2) tartományban értelmezett $\begin{array}{c}{\displaystyle \frac{2T}{n\pi }=f\left(x\right)=x^2-\frac{4R}{n}x+\frac{2R^2}{n}={\left(x-\frac{2R}{n}\right)}^2+\frac{2\left(n-2\right)R^2}{n^2}}\end{array}$ függvénynek. $f\left(x\right)$-et minden $x$-re értelmezett függvénynek tekintve (rögzített $n$ mellett) minimuma van az $\begin{array}{c}{\displaystyle x_0=\frac{2R}{n}}\end{array}$ helyen, és a minimum értéke az állandó tag, pozitív.   2. Megmutatjuk, hogy $x_0$ benne van a (2) intervallumban, tehát feladatunk b) részére a válasz éppen $x_0$. Az $\frac{a}{2}\geqq x_0$ egyenlőtlenség ekvivalens evvel: $\frac{n}{2}\cdot a\geqq 2R$, vagyis, hogy a szabályos $n$-szög $\left(n\geqq 3\right)$ kerületének a fele nagyobb az átmérőnél. Páros $n$ esetén ez szinte nyilvánvaló: a kerület felét megadja $\frac{n}{2}$ számú, egymás után csatlakozó oldalból álló töröttvonal, és az ennek végpontjait összekötő átló hossza éppen az átmérő. Páratlan $n$ esetén a kerület felét egy $A$ csúcstól a szemben levő oldal $D$ felezőpontjáig haladva tesszük meg (bármelyik irányban), és akkor az $AD$ egyenes mint szimmetriatengely átmegy $O$-n (2. ábr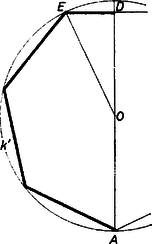a).     2. ábra   Az egyik $A\text{...}D$ félkerületet két részre osztjuk a $D$-vel megfelezett oldal $E$ végpontjával. Az $AE$ útrész vetülete a tengelyre $AD=AO+OD$ (hiszen $O$ a sokszögnek belső pontja). A vetület nem nagyobb, mint az eredeti útrész, ezért $\begin{array}{c}{\displaystyle \frac{n}{2}a=A\text{...}E+ED>AO+\left(OD+ED\right)>R+OE=2R\mathrm{,}}\end{array}$ ezt akartuk bizonyítani. (Egyenlőség semmilyen $n$-re nem teljesülhet.) (2)-ből az $x_0\geqq R-r$ rész belátásához tekintsük az $F$ pont körül azt a $k_1$ kört, amely érinti a sokszögünk köré írt $k\text{'}$ kört, nyilvánvalóan az $AB$ ív $H$ felezőpontjában (1. és 3. ábra). 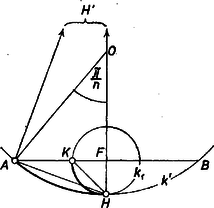    3. ábra   Az $FA$ félegyenest $k_1$ az $F$ és $A$ közti $K$ pontban metszi, mert $\begin{array}{c}{\displaystyle KF+FO=HF+FO=HO=AO<AF+FO\mathrm{,}}\end{array}$ tehát $KF<AF$, és így $KH<AH$. Fogadjuk el ebből bizonyítás nélkül, hogy $k\text{'}$-nek $AH$ húrhoz tartozó íve hosszabb, mint $k_1$-nek a $KH$ húrhoz tartozó negyedköríve: $\begin{array}{c}{\displaystyle \widehat{AH}>\widehat{KH}\mathrm{,}\text{ azaz}R\frac{\pi }{n}>\frac{\pi }{2}FH=\frac{\pi }{2}\left(OH-OF\right)=\frac{\pi }{2}\left(R-r\right)\mathrm{.}}\end{array}$ Ebből $2/\pi$-vel való szorzás útján adódik a kívánt egyenlőtlenség: $\begin{array}{c}{\displaystyle \frac{2R}{n}=x_0>R-r\mathrm{.}}\end{array}$ Az eddigiek szerint a sokszög területéből a megrajzolt $\left(1+n\right)$ kör által lefedett rész minimális, ha a sokszög $n$ csúcsa körül leírt körök sugara $x_0$, egyenlő a $k\text{'}$ kör átmérőjének $n$-ed részével. A sugár szerkesztése nyilvánvaló, és ezzel $\varrho$ is kiadódik. 3. Azt is láttuk, hogy $x_0$ a (2)-beli korlátok egyikével sem egyenlő. Legyen az alsó korlát $R-r=x_1$, a felső korlát $a/2=x_2$. Így $f\left(x\right)$ az $x_0$-tól $x_1$ felé haladva is, $x_2$ felé haladva is növekszik és a másodfokú függvény grafikonjának szemléletére támaszkodva mondhatjuk, hogy legnagyobb elért értéke az első esetben $f\left(x_1\right)$, a másodikban $f\left(x_2\right)$. Eszerint $f$-nek az $\left(x_1\mathrm{,}{x}_2\right)$ intervallumon elért maximuma e két érték nagyobbika. Mármost $\begin{array}{c}{\displaystyle f\left(x_2\right)-\left(f{x}_1\right)={\left(x_2-x_0\right)}^2-{\left(x_1-x_0\right)}^2\mathrm{,}}\end{array}$ és ez aszerint pozitív, negatív vagy 0, hogy $|x_2-x_0|=x_2-x_0$ és $|x_1-x_0|=$ $=x_0-x_1$ közül az első, illetve a második a nagyobb, illetve ha éppen egyenlők. Megmutatjuk, hogy $n=3$ esetén az $f\left(x_2\right)$-ből adódó $T=\frac{n\pi }{2}f\left(x_2\right)$ a maximum, $n=4$ esetén $f\left(x_1\right)=f\left(x_2\right)$, vagyis $\begin{array}{c}{\displaystyle x_1=R-\frac{R}{\sqrt[]{2}}\mathrm{,}{\varrho }_1=\frac{R}{\sqrt[]{2}}\mathrm{,}\text{és}{x}_2=\frac{a}{2}=\frac{R}{\sqrt[]{2}}={\varrho }_1\mathrm{,}}\end{array}$ és ${\varrho }_2=R-x_2=x_1$ mellett egyaránt maximumot kapunk, $n\geqq 5$ mellett pedig $f\left(x_1\right)$ vezet a maximumra. Valóban, $n=3$ esetén $a=R\sqrt[]{3}$, $r=R/2$, így ${\displaystyle \begin{array}{c}\hfill {\displaystyle x_0-x_1=\frac{2R}{3}-\left(R-\frac{R}{2}\right)=\frac{R}{6}\mathrm{,}}\hfill \\ \hfill {\displaystyle x_2-x_0=\frac{R\sqrt[]{3}}{2}-\frac{2R}{3}=\frac{R}{6}\left(\sqrt[]{27}-4\right)>\frac{R}{6}\left(5-4\right)=x_0-x_1\mathrm{.}}\hfill \end{array}}$ A legnagyobb lefedését tehát úgy kapjuk az $a$ oldalú szabályos háromszögnek, ha a csúcsai körül $a/2$ sugarú köröket írunk, középpontja körül pedig azt a $k$-t, amely e három kört érinti (4. ábra első háromszöge, a második ábra $f\left(x_1\right)$-et, a harmadik a minimális fedést mutatja). 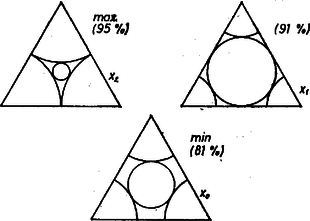    4. ábra   Az $n=4$ melletti $f\left(x_1\right)=f\left(x_2\right)$ belátásához elég a négyzetet $x_1$ és $x_2$ esetében egyaránt 4‐4 egybevágó részre osztani a két oldalfelezővel, a részek átrendezésével egymásba mennek át (5. ábra, a szintén bemutatott minimum esetében 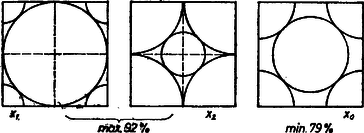$\varrho =x_0$).     5. ábra   Az $n=5$ esetre a trigonometriai táblázat adatait használjuk fel. Mindig érvényes, hogy 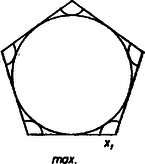$\begin{array}{c}{\displaystyle r=R\text{cos}\frac{\pi }{n}\mathrm{,}\frac{a}{2}=R\text{sin}\frac{\pi }{n}\mathrm{,}}\end{array}$ és mivel $n=5$ mellett $\text{cos}{36}^{\circ }>0\mathrm{,}8=\frac{4}{5}$ és $\text{sin}{36}^{\circ }>0\mathrm{,}6=\frac{3}{5}$, azért ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle x_0-x_1=R\left(\frac{2}{5}-1+\text{cos}{36}^{\circ }\right)>\frac{R}{5}\mathrm{,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle x_2-x=R\left(\text{sin}{36}^{\circ }-\frac{2}{5}\right)<\frac{R}{5}\mathrm{,}}\hfill \end{array}}$ tehát $f\left(x_1\right)>f\left(x_2\right)$, a lefedés maximumát úgy kapjuk, hogy $k$-ként a szabályos ötszög beírt körét vesszük (6. ábra).     6. ábra   Végül az $n>5$ értékekre jelöljük $H$-nak $k\text{'}$-beli átellenes pontját $H\text{'}$-vel. Az $AHH\text{'}$ derékszögű háromszög felhasználásával ${\displaystyle \begin{array}{c}\hfill {\displaystyle d=|x_1-x_0|-|x_2-x_0|=2x_0-\left(x_1+x_2\right)=2x_0-\left(FH+AF\right)=}\hfill \\ \hfill {\displaystyle =\frac{4R}{n}-\left(\frac{A{H}^2}{HH\text{'}}+AF\right)=\frac{4R}{n}-\left(\frac{A{H}^2}{2R}+AF\right)\mathrm{.}}\hfill \end{array}}$ A kivonandót növeljük, ha $AF$ helyére az $AH$ húrt írjuk, majd mindkét tagban az $AH$ húr helyére az $AH=R\frac{\pi }{n}$ ívet: $\begin{array}{c}{\displaystyle \frac{d}{R}>\left(\frac{4}{n}-\frac{{\pi }^2}{2n^2}+\frac{\pi }{n}\right)=\frac{1}{n}\left(4-\pi -\frac{{\pi }^2}{2n}\right)>\frac{0\mathrm{,}02}{n}>\mathrm{0,}}\end{array}$ (a zárójelben ${\pi }^2$-t 10-re növeltük és $n$-et 6-ra csökkentettük). Ezzel az előrebocsátottak szerint megmutattuk, hogy minden $n\geqq 5$ esetre úgy adja a rajzolt körrendszer a szabályos $n$-szög maximális lefedését, ha $k$-ként a beírt körből indulunk ki.    Brindza Béla (Csongrád, Batsányi J. Gimn., IV. o. t.)