Feladat: F.2003 Korcsoport: 16-17 Nehézségi fok: -
Megoldó(k):  Ambrus A. ,  Bíró Cs. ,  Bodó Z. ,  Bozai É. ,  Cserjési J. ,  Csikós B. ,  Fridli S. ,  Fried M. ,  Gál 327 L. ,  Gál B. ,  Holop L. ,  Homonnay G. ,  Horváth 712 I. ,  Hunyadi L. ,  Jónás B. ,  Kereszti L. ,  Knébel I. ,  Koltay K. ,  Kormos Z. ,  Magyar Z. ,  Miklós D. ,  Moussong G. ,  Nagy 578 I. ,  Nőthig L. ,  Pörneczi T. ,  Rapai T. ,  Rigó I. ,  Soukup L. ,  Szabó 719 K. ,  Szőke R. ,  Vindics J. ,  Wolf György 
Füzet: 1976/március, 99 - 100. oldal  PDF  |  MathML 
Témakör(ök): Geometriai egyenlőtlenségek, Indirekt bizonyítási mód, Logikai feladatok, Teljes indukció módszere, Feladat
Hivatkozás(ok):Feladatok: 1975/október: F.2003

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladatnál kissé általánosabban azt mutatjuk meg, hogy n piros és n kék pont esetén is létezik a kívánt összekötő rendszer, ahol n≥1 tetszőleges egész szám.

 

I. megoldás. A bizonyítást teljes indukcióval végezzük. Ha n=1, az állítás triviálisan igaz. Tegyük fel, hogy az állítást valamilyen n-ig már minden számra beláttuk. Megmutatjuk, hogy ebből az (n+1)-re is következik.
Tekintsük az összes olyan szakaszt, amelyek egyik végpontja piros, a másik kék pont. Azt fogjuk megmutatni, hogy ezek között van olyan, mondjuk AB, hogy az AB egyenes úgy vágja ketté a pontjainkat, hogy a piros és kék pontok száma a keletkező részeken belül is egyenlő. Az indukciós feltevésünk szerint e részeken belül már összeköthetőek a pontok a kívánt módon. Mivel a kapott szakaszoknak nincs közös pontjuk az AB szakasszal, azokat az AB szakasszal kiegészítve az egész pontrendszernek egy megfelelő összekötését kapjuk.
Vegyünk fel egy tetszőleges koordináta‐rendszert, és válasszuk ki a pontjaink közül a legkisebb ordinátájút, legyen ez A. (Ha a legkisebb ordinátához több pont is tartozna, A legyen közülük a legkisebb abcisszájú.) Legyen mondjuk ez az A pont piros. Jelöljük a-val az A-n átmenő, x tengellyel párhuzamos egyenest, és tekintsük az A-ból a többi pont felé futó félegyeneseket. Ezek mind a-n vagy a fölött vannak, és mindegyikük pontosan egy A-tól különböző pontot tartalmaz, hiszen feltevésünk szerint pontjaink közt nincs három egy egyenesen. Vegyük a-nak az x tengely pozitív irányába mutató felét, és forgassuk ezt a félegyenest A körül pozitív irányba. Jelöljük a pontrendszer pontjait abban a sorrendben, ahogy találkozunk velük B1-gyel, B2-vel, ..., B2n-1-gyel (1. ábra).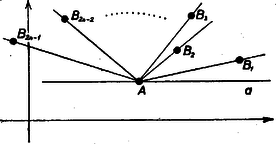
 

 

1. ábra
 

Ha B1 vagy B2n-1 kék, a keresett AB szakasz szerepére választhatjuk az AB1, illetve AB2n-1 szakaszt.
Ha B1 és B2n-1 is piros, tekintsük a B1AB2, B1AB3, ..., B1AB2n-1 szögtartományokat határaikkal együtt, és nézzük meg, hogy mennyi az általuk tartalmazott piros és kék pontok számának (előjeles) különbsége. A tartományok közül az elsőben, a B1AB2 tartományban ez a különbség 1 vagy 3, tehát pozitív, az utolsóban, B1AB2n-1-ben nulla, emiatt az utolsó előttiben -1. Mivel az egymás után következő tartományok között a különbség mindig 1-gyel változik, kell lennie egy olyan tartománynak, ahol a különbség 0, legyen B1ABk az első ilyen tartomány (1<k<2n-1). Ekkor Bk csak kék lehet, hiszen B1ABk-1-ben a piros és kék pontok számának a különbsége még pozitív. Most tehát ABk választható a keresett AB szakasznak, a bizonyítást ezzel befejeztük.
 

Megjegyzés. A fenti alapgondolat teljes indukció nélkül is megfogalmazható, a ponthalmaz ismételt (legfeljebb (n-1)-szeri felosztásával. Magában az alkalmazott indukcióban nem lett volna elég a szokásos "ha n-re igaz, (n+1)-re is igaz'' típusú meggondolás, hiszen a kettévágásnál n-nél kevesebb pontot is kaphatunk.
 

II. megoldás. Képzeljük el az összes összekötő rendszert, amelyek egy‐egy kék és piros pontot kapcsolnak össze. Ezek száma 2n pont esetén n!, tehát véges érték. Ezek között nyilvánvalóan van egy, vagy több olyan rendszer, ahol az összes résztvevő szakaszok hosszúságainak összege minimális.
Tegyük fel most, hogy a bizonyítandó állítás nem igaz. Ekkor kiválasztva a minimális összegű összekötést (vagy egyet a minimálisak közül), abban biztosan van legalább két metsző szakasz. Legyenek ezek AB és CD ‐ ahol A és C pont kék, B és D pedig piros (2. ábra).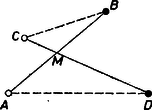
 

 

2. ábra
 

Módosítsuk úgy a rendszert, hogy a szaggatott vonal szerint A-t D-vel, B-t C-vel kötjük össze. Ha a metszéspont M, a háromszög‐egyenlőtlenség miatt igaz a következő:
AM+MD>AD,CM+MB>CB.
E kettőt összegezve:
AM+MB+CM+MD=AB+CD>AD+CB.
Vagyis a rendszer nem volt minimális, hiszen annál kisebbet találtunk. Ellentmondásra jutottunk, ezzel igazoltuk az állítást.