| Feladat: | F.2000 | Korcsoport: 16-17 | Nehézségi fok: - |
| Füzet: | 1976/január, 13 - 15. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Egyenes, Diszkusszió, Háromszögek szerkesztése, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1975/szeptember: F.2000 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Felvéve a oldalegyenest, nyilvánvaló, hogy az csúcs az ezzel párhuzamos, tőle távolságban haladó egyenesen lesz, az oldal felezőpontja pedig, amelyre , az és között, tőlük egyenlő távolságban haladó egyenesen. Ma még az -en tetszőlegesen megválasztott körüli sugarú körívvel kimetsszük -ból helyzetét, hosszúságadatainkat felhasználtuk. 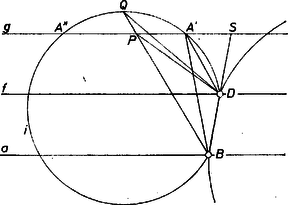 1. ábra Eszerint a látószög csak a -n és -n átmenő, -t érintő körök , ill. érintési pontjaiban lehet maximális. Ilyen kör a egyenes mindkét partján várható, megszerkesztésükhöz mindjárt felhasználhatjuk az előbbi -t tartalmazó kört. Legyen ugyanis a és egyenesek metszéspontja , így ismert tétel szerint , azaz az , szakaszok mértani középarányosa, és ugyanezen feltétel szerint hosszát megadja bármely, a , pontokon átmenő körhöz -ből szerkesztett érintőszakasz hossza. Eszerint megszerkesztve, az -ből a -hoz húzott érintők egyikét ‐ érintési pontja legyen ‐, az körüli, -n átmenő kör kimetszi -ből -et és -t. Ezekből a háromszög hátralevő csúcsának , helyzetét a -re való tükrözéssel kapjuk. 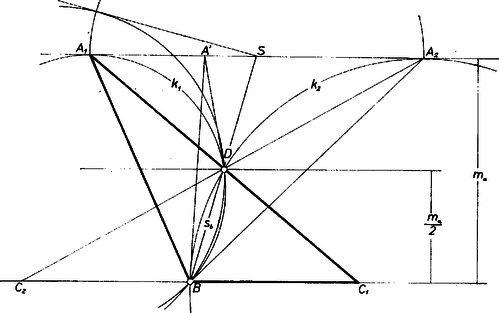 2. ábra Az előzőek azt bizonyítják, hogy a -n haladó pontból a szakasz látószögének -ben vagy -ben van maximuma. Ugyanis miatt valamelyik érintési pont az között van és játszhatja szerepét. Az viszont, hogy a és szögek közül melyik a nagyobb ‐ hiszen nyilván ezt keressük ‐, külön kell eldöntenünk. Nyilvánvalóan egyenlő e két szög, ha merőlegesen áll -re , de így szimmetriatengellyé válik és a két megoldás úgysem számít különbözőnek. Máskülönben válasszuk úgy az indexeket, hogy legyen, megmutatjuk, hogy így . Valóban, -nek a tengelyre való tükörképe -nek -t nem tartalmazó partján van, így az , , pontokkal meghatározott kör két pontban metszi -t (a -vel párhuzamos egyenes két partján), így a nem lehet maximális, hiszen rajta van azon a húron, amit e körből kimetsz. Nyilvánvaló az eddigiekből, hogy feladatunkból a legnagyobb szögre vonatkozó rész megoldhatóságának egyetlen feltétele , és ekkor a megoldás egyértelmű. A legkisebb szögre vonatkozó részre válaszunk: ilyen háromszög nincs, hiszen amíg , addig helyére (amennyiben a fenti szakaszon van) az szakasz egy belső pontját véve, ; ha viszont azonos -sel, akkor a háromszög elfajul egyenesszakasszá, az magasság értelmét veszti. Megjegyzés. Az mértani közép természetesen máshogyan is szerkeszthető, többek között a nyilvánvaló |