| Feladat: | F.1999 | Korcsoport: 18- | Nehézségi fok: - |
| Füzet: | 1976/január, 12 - 13. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Egyenesek egyenlete, Parabola egyenlete, Parabola, mint mértani hely, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1975/szeptember: F.1999 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Helyezzük el koordináta-rendszerünket úgy, hogy a parabola csúcsérintője az tengellyel, a parabola tengelye az tengellyel essék egybe, az egységet pedig válasszuk meg úgy, hogy a parabola fókuszának két koordinátája legyen. Ekkor a parabola egyenlete: , vezéregyeneséé . 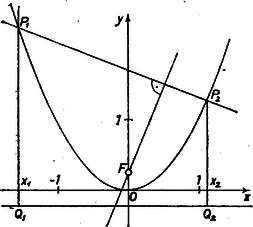 Így a parabola tetszőleges két pontjának koordinátái , . A , pontokra illeszkedő egyenes meredeksége Írjuk fel az -en átmenő, egyenesre merőleges egyenes egyenletét. Ha , akkor e merőleges egyenes meredekségét -vel jelölve igaz, hogy , azaz . Az egyenes az tengelyt az pontban metszi, így egyenlete:
Ha , vagyis , akkor a egyenes párhuzamos az tengellyel, így a rá merőleges egyenes párhuzamos az tengellyel. Mivel illeszkedik az tengelyre, ezért ez az egyenes maga az tengely. A , szakasz felezőpontja ekkor a pont, vagyis ez a pont az tengelyen van, ezért az állítás akkor is igaz. Ezzel a bizonyítandó állítást , minden értékpárjára bizonyítottuk. II. megoldás. A parabola definíciójából következik, hogy . Tekintsük a középpontú sugarú kört! A egyenes e körnek szimmetriatengelye, ezért a kör bármely pontját tükrözve rá, e körön levő pontot kapunk. Tükrözzük -et -re, a (tőle nem feltétlenül különböző) tükörképét jelöljük -vel. 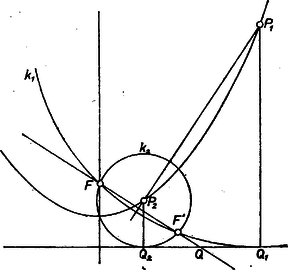 Így , és rajta van a -re merőleges, -re illeszkedő egyenesen. Ennek az egyenesnek, és a parabola vezéregyenesek metszéspontja legyen . ( csak akkor nem létezne, ha e két egyenes párhuzamos lenne, azaz merőleges lenne a vezéregyenesre, ez azonban lehetetlen, mert bármely, a vezéregyenesre merőleges egyenesen csak egy pontja van a parabolának.) Ekkor -nak a körre vonatkozó hatványa: . Hasonlóan a középpontú, -en átmenő körre vonatkozó hatvány: , azaz , ami ekvivalens az állítással. |