Kezdőlap


Feladat:	F.1998	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Kramarics Géza
Füzet:	1976/január, 11 - 12. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Háromszögek nevezetes tételei, Súlyvonal, Koszinusztétel alkalmazása, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1975/szeptember: F.1998

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha valamely $A B C$ háromszögben $A B > B C$ , akkor a $B$ csúcs az $A C$ szakasz felező merőlegesének azon az oldalán van, ahol $C$ . Itt van a háromszög $B$ -hez tartozó súlyvonala, és rajta a háromszög $S$ súlypontja is, tehát $A S > S C$ , vagyis a háromszög $A$ -beli $s_{a}$ súlyvonala hosszabb a $C$ -beli $s_{c}$ -nél.
Válasszuk úgy a vizsgált háromszög betűzését, hogy az oldalak hosszára $a \leq b \leq c$ teljesüljön, ekkor $s_{a} \geq s_{b} \geq s_{c}$ . Ha tehát a súlyvonalakból alkotott háromszög hasonló az eredetihez, akkor van olyan $λ$ szám, hogy

\begin{matrix} s_{a} = λ c, s_{b} = λ b, s_{c} = λ a . \end{matrix}

(1)

Tükrözzük

B

-t az

A C

szakasz felezőpontjára, kapjuk

D

-t. Jelöljük a

B C

C D

szakaszok felezőpontját

A_{1}

-gye1, illetve

C_{1}

-gyel. Mivel

A_{1} C_{1} = \frac{1}{2} B D = s_{b}

A C_{1} = s_{c}

, az

A A_{1} C_{1}

háromszög az, amit a súlyvonalakból szerkeszthetünk.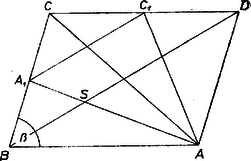

Ha ezt elhagyjuk az

A B C D

paralelogrammából, a visszamaradó

A B A_{1} A D C_{1}

darabok területe az eredeti háromszög területének a felével,

A_{1} C C_{1}

területe pedig a negyedével egyenlő. Ha tehát az eredeti háromszög

T

-vel, a súlyvonalakból alkotható háromszög területét

t

-vel jelöljük, akkor

2 T = t + T + \frac{1}{4} T

, vagyis

4 t = 3 T

. Mivel (1) szerint

t = λ^{2} T

\begin{matrix} λ = \frac{\sqrt[]{3}}{2}, \end{matrix}

(2)

Jelöljük az

A B C

háromszög

B

-nél levő szögét

β

-val, akkor

B C D ∢ = 180^{\circ} - β

, és a cosinus-tétel alapján

\begin{matrix} b^{2} = a^{2} + c^{2} - 2 a c cos & β \\ 4 s_{b}^{2} = a^{2} + c^{2} + 2 a c cos & β . & (3) \end{matrix}

Adjuk össze ezt a két egyenletet, és

4 s_{b}^{2}

helyére (1) és (2) alapján írjunk

3 b^{2}

-t kapjuk, hogy

4 b^{2} = 2 a^{2} + 2 c^{2}

, azaz

\begin{matrix} 2 b^{2} = a^{2} + c^{2} \end{matrix}

(4)

amint azt bizonyítani akartuk.

Kramarics Géza (Zalaegerszeg, Zrínyi M. Gimn., IV. o. t.)

Megjegyzés. A most bizonyított állítás meg is fordítható: ha egy háromszög oldalaira teljesül (4), akkor a súlyvonalakból szerkesztett háromszög hasonló az eredetihez. Azt, hogy (4)-ből

4 s_{b}^{2} = 3 b^{2}

következik, (3)-ból közvetlenül megkapjuk, a

4 s_{c}^{2} = 3 a^{2}

4 s_{a}^{2} = 3 c^{2}

igazolásához pedig a (3)-hoz hasonlóan bizonyítható

\begin{matrix} 4 s_{c}^{2} = 2 a^{2} + 2 b^{2} - c^{2}, 4 s_{a}^{2} = 2 b^{2} + 2 c^{2} - a^{2} \end{matrix}

összefüggéseket kell felhasználnunk. A megfordításhoz azonban (4) önmagában nem elég, előfordulhat ugyanis, hogy (4) teljesül, de nincs olyan háromszög, amelynek

a

b

c

volna az oldala, például

a = 1

b = 5

c = 7

mellett.