Kezdőlap


Feladat:	F.1975	Korcsoport: 18-	Nehézségi fok: -
Füzet:	1976/szeptember, 9 - 12. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenletrendszerek, Pont körüli forgatás, A háromszögek nevezetes pontjai, Terület, felszín, Koszinusztétel alkalmazása, Síkbeli szimmetrikus alakzatok, Feladat
Hivatkozás(ok):	Feladatok: 1975/február: F.1975

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az $A B C$ háromszögben $B C = a = 79$ , $C A = b = 65$ , $A B = c = 47$ egység, a szóban forgó pont $P$ , és $P A = x$ , $P B = y$ , $P C = z$ . Pontunk semmiféle háromszög esetében sem lehet kívül a háromszögön, különben ugyanis két oldal látószöge együtt egyenlő lenne a harmadik látószöggel, akár valamelyik szög csúcstartományában próbálnánk fölvenni $P$ -t, akár valamelyik oldalával szomszédos, végtelenbe nyúló ún. serpenyőtartományában; így pedig nem lehet egyenlő a három látószög. Hasonlóan nem lehet $P$ a háromszög kerületén sem.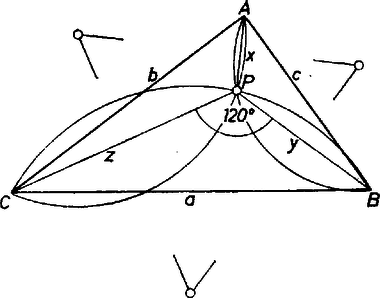
Eszerint a látószögek összege $360^{\circ}$ , és mindegyiknek $120^{\circ}$ az értéke, és $P$ -t szerkesztéssel úgy kapjuk, hogy vesszük két oldalszakasz $120^{\circ}$ -os nyílású látókörívét azon a partjukon, amelyikben a háromszög van, ezek közös pontja $P$ . (1. ábra.)

1. ábra

Alkalmazzuk a cosinustételt egymás után a

P B C

P C A

P A B

háromszögnek

P

-vel szemben levő oldalára. A

P

-nél levő szög cosinusa mindegyikben

(- 0,5)

, így

\begin{matrix} x^{2} + y^{2} + x y = c^{2}, & (1) \\ y^{2} + z^{2} + y z = a^{2}, & (2) \\ z^{2} + x^{2} + z x = b^{2} . & (3) \end{matrix}

Vonjunk ki egyrészt

(2)

-ből

(3)

-at, másrészt

(3)

-ból

(1)

-et:

\begin{matrix} y^{2} - x^{2} + z (y - x) = (y - x) (x + y + z) = a^{2} - b^{2}, & (4) \\ z^{2} - y^{2} + x (z - y) = (z - y) (x + y + z) = b^{2} - c^{2} . & (5) \end{matrix}

Itt célszerű feladnunk az általános megoldás keresését, ugyanis az oldalak adott mértékszámai jelentős könnyítést adnak azzal, hogy legutóbbi két egyenletünk jobb oldala egyenlő:

\begin{matrix} a^{2} - b^{2} = 79^{2} - 65^{2} = 2016 = 65^{2} - 47^{2} = b^{2} - c^{2} . \end{matrix}

Így

(4)

és

(5)

bal oldalainak egyenlőségéből

x + y + z > 0

miatt

\begin{matrix} y - x = z - y > 0, \end{matrix}

vagyis

x

y

és

z

ebben a sorrendben növekvő számtani sorozatot alkot. Ezért a három ismeretlen összege

(4)

-ben és

(5)

-ben

3 y

, ezt és a számadatokat behelyettesítve

\begin{matrix} y - x = z - y = \frac{2016}{3 y} = \frac{672}{y} . \end{matrix}

Innen a sorozat mindkét szélső tagja kifejezhető a középsővel:

\begin{matrix} x = y - \frac{672}{y} = \frac{y^{2} - 672}{y}, z = y + \frac{672}{y} = \frac{y^{2} + 672}{y}, \end{matrix}

(6)

és ezeket

(3)

-ba helyettesítve

y^{2}

-re másodfokú egyenletet kapunk:

\begin{matrix} {(y^{2} + 672)}^{2} + {(y^{2} - 672)}^{2} + (y^{4} - 672^{2}) = {(65 y)}^{2}, \\ 3 y^{4} - 65^{2} y^{2} + 672^{2} = 0, \\ y^{2} = \frac{1}{6} (4225 \pm \sqrt[]{12 431 617}) = {\binom{1291, 8,}{611, 5.} \end{matrix}

Természetesen elég vennünk

y

pozitív értékeit:

\begin{matrix} y_{1} = 35, 94, y_{2} = 10, 79. \end{matrix}

(6)

-ba leendő behelyettesítés céljára

672 / y_{1} = 18, 70

672 / y_{2} = 62, 26

, és az előbbi alapján a keresett távolságok:

\begin{matrix} x = P A = 17, 24, y = P B = 35, 94, z = P C = 54, 61 egység. \end{matrix}

A másik megoldás:

x_{2} = - 51, 46

y_{2} = 10, 79

z_{2} = 73, 04

, ha

x_{2}

abszolút értékét vesszük, szintén meghatározza a sík egy

P_{2}

pontját (2. ábra).

2. ábra

Előre tudjuk, hogy ez nem felel meg feladatunk geometriai kérdésének, de hozzátehetjük: így az

A B

és

A C

oldalak látószögének cosinusa

(1)

ill.

(3)

szerint

+ 0, 5

, e két látószög

60^{\circ}

, a

B C

oldalé

120^{\circ}

, amazok összege.

P_{2}

annak a 3 körívnek a közös pontja, amelyek az 1. ábrabelieknek tükörképei a megfelelő oldalra. (Eszerint

x_{2}

-t alaposabb indokolással mellőztük, mint a két

y^{2}

érték negatív négyzetgyökét. Egyébként e negatív négyzetgyökökkel

x

és

z

csupán előjelet változtatnak, és ismét az eddigi két megoldásra jutunk.)
Megjegyzés. A talált

P

pontot a látószögek egyezése alapján tetszőleges

A B C

háromszögben a háromszög izogonális pontjának nevezik.

II. megoldás. Illesszünk a vizsgált háromszög oldalaihoz kifelé szabályos háromszögeket, és jelöljük ezek

A

-val,

B

-vel,

C

-vel szemközti csúcsait rendre

A_{1}

-gyel,

B_{1}

-gyel,

C_{1}

-gyel. Ha az eredeti háromszög

A

-nál levő szöge kisebb

120^{\circ}

-nál, akkor az

A C

egyenest

A B

-n keresztül

A C_{1}

-be vivő forgatás kisebb

180^{\circ}

-nál, tehát

C_{1}

A C

egyenesnek ugyanazon az oldalán van, mint

B

. Ha az

A B C

szög is kisebb

120^{\circ}

-nál, akkor

C_{1}

B C

egyenesnek is ugyanazon az oldalán van, mint az eredeti háromszög, tehát a

C C_{1}

szakasz metszi az

A B

oldalt. Ha pedig az eredeti háromszög minden szöge kisebb

120^{\circ}

-nál, akkor ugyanígy kapjuk az

A A_{1}

B B_{1}

szakaszokra, hogy metszik a szemközti oldalt, tehát rendre egymást is metszik. Megmutatjuk, hogy ekkor e három szakasz egy ponton megy át, és ez a keresett

P

pont.
Forgassuk el az

A B B_{1}

háromszöget

A

körül úgy, hogy

B

C_{1}

-be kerüljön. Akkor a

B_{1}

C

-be megy át, tehát a

B B_{1}

C C_{1}

szakaszok

M

metszéspontjából az

A B

B C

oldalak

120^{\circ}

-os szög alatt látszanak. Eszerint

M

rajta van az I. megoldás elején említett két

120^{\circ}

-os látókörön, tehát valóban azonos

P

-vel. Mivel ez a

C C_{1}

A A_{1}

, valamint az

A A_{1}

B B_{1}

szakaszok metszéspontjáról is elmondható, mindhárom szakasz átmegy

P

-n.

Mérjük fel a

P B_{1}

szakaszra

P

-ből kiindulva a

P D = P A = x

szakaszt. Mivel

A P B_{1} ∢ = 60^{\circ}

, az

A P D

háromszög szabályos, így

A D = x

. Forgassuk el

A

körül az

A P C

háromszöget

60^{\circ}

-kal úgy, hogy

P

D

-be kerüljön, akkor

C

B_{1}

-be jut, tehát

D B_{1} = P C = z

. Ezek szerint

\begin{matrix} B B_{1} = B P + P D + D B_{1} = y + x + z = w, \end{matrix}

és hasonlóan kapjuk, hogy

A A_{1} = C C_{1} = w

.
Jelöljük az

A_{1} B C

háromszög köré írt kört

k

-val, középpontját

O

-val, sugarát

r

-rel. Könnyen látható, hogy

r = \frac{a}{\sqrt[]{3}}

. Alkalmazzuk a körhöz külső pontból húzott szelő darabjaira vonatkozó tételt a

k

kör

A A_{1}

szelőjére, kapjuk, hogy

\begin{matrix} x \cdot w = \bar{A P} \cdot \bar{A A_{1}} = \bar{A O^{2}} - r^{2} . \end{matrix}

A O

szakasz hosszát meghatározhatjuk abból a derékszögű háromszögből, amelynek

A O

az átfogója, és az

O

-hoz csatlakozó befogója párhuzamos

B C

-vel. Ennek másik befogója az eredeti háromszög

A

-beli magasságvonalán van, jelöljük ennek

B C

-n levő pontját

G

-vel, a derékszög csúcsát

H

-val,

B C

felezőpontját

F

-fel,

A G

-t

m

-mel,

F G

-t

d

-vel:

\begin{matrix} \bar{A O^{2}} = \bar{A H^{2}} + \bar{H O^{2}} = {(m + \frac{r}{2})}^{2} + d^{2} = (m^{2} + d^{2}) + r m + \frac{r^{2}}{4} = \bar{A F^{2}} + \frac{a m}{\sqrt[]{3}} + \frac{a^{2}}{12} . \end{matrix}

Használjuk még fel, hogy az

A F

súlyvonalra

\begin{matrix} \bar{A F^{2}} = \frac{2 b^{2} + 2 c^{2} - a^{2}}{4} \end{matrix}

teljesül, kapjuk, hogy

\begin{matrix} x w = \frac{2 b^{2} + 2 c^{2} - a^{2}}{4} + \frac{2 t}{\sqrt[]{3}} + \frac{a^{2}}{12} - \frac{a^{2}}{3} = \frac{2 t}{\sqrt[]{3}} + \frac{b^{2} + c^{2} - a^{2}}{2}, \end{matrix}

ahol

t = \frac{1}{2} a \cdot m

a háromszög területe.
Hasonlóan kapjuk, hogy

\begin{matrix} y w = \frac{2 t}{\sqrt[]{3}} + \frac{c^{2} + a^{2} - b^{2}}{2}, z w = \frac{2 t}{\sqrt[]{3}} + \frac{a^{2} + b^{2} - c^{2}}{2}, \end{matrix}

tehát

\begin{matrix} w^{2} = (x + y + z) w = 2 \sqrt[]{3 t} + \frac{a^{2} + b^{2} + c^{2}}{2} . \end{matrix}

Ebből négyzetgyökvonással kapjuk

w

értékét, és ezt az

x w

y w

z w

szakaszokra vonatkozó összefüggésekbe helyettesítve kapjuk az

x

y

z

távolságokat. Ha ‐ mint esetünkben ‐ az eredeti háromszögben a három oldal nagysága adott, akkor

t

értékét a Heron-képletből számíthatjuk.

\begin{matrix} t = \sqrt[]{s (s - a) (s - b) (s - c)} = \frac{1}{4} \sqrt[]{191 \cdot 33 \cdot 61 \cdot 97} = 1526, 74, \end{matrix}

tehát

\begin{matrix} x w & = 1859, 43 \\ y w & = 3875, 43 \\ z w & = 5891, 43 \\ w & = 11626, 29 = 107, 83 \\ x & = 17, 24; y = 35, 94; z = 54, 64. \end{matrix}

Számolás közben láttuk, hogy mindegyik oldal négyzete kisebb a másik két oldal négyzetének összegénél, így a vizsgált háromszög hegyesszögű. Emiatt az elmondottak érvényesek rá, a

P

pont létrejön, és a kapott eredmények helyesek.