Feladat: F.1974 Korcsoport: 16-17 Nehézségi fok: -
Megoldó(k):  Jakab Tibor 
Füzet: 1976/január, 5 - 6. oldal  PDF  |  MathML 
Témakör(ök): Szimmetrikus sokszögek, Szabályos sokszögek geometriája, Feladat
Hivatkozás(ok):Feladatok: 1975/február: F.1974

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Azt fogjuk bebizonyítani, hogy MN párhuzamos a C2C5 átlóval; ez ekvivalens az állítással, hiszen OC0 a hétszögnek szimmetriatengelye, és C2, C5 erre tükrös pontpár.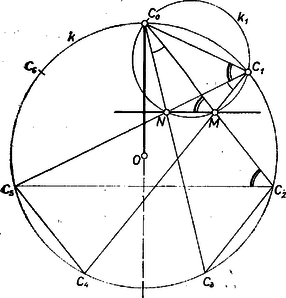

 

 

Az MN szakaszt C0-ból és C1-ből egyenlő szögek alatt látjuk, mert a két látószög a hétszög köré írt k kör rövidebbik C2C3, illetve C4C5 ívén nyugvó kerületi szög, és a két ív egyenlő. Ezért a C0, N, M, C1 pontok egy k1 körön vannak, és C1 is, M is a C0N, azaz C0C3 egyenesnek ugyanazon a partján van.
Így C0MN∢=C0C1N∢=C0C1C5∢, és az utóbbi szög tovább k révén a C0C2C5∢-gel egyenlő, tehát a közös szárú C0MN és C0C2C5 szögek egyenlők. És mivel N és C5 a közös szárnak ugyanazon a partján vannak, azért a két szög egyállású, valóban MN||C2C5⊥OC0.
 

Jakab Tibor (Budapest, Berzsenyi D. Gimn., IV. o. t.)

 

Megjegyzés. A kerületi szögek tételeinek egy szokásos átfogalmazása a következő: tetszőleges C0C1P0 háromszög C0P0 egyenesét C0 körül és C1P0 egyenesét C1 körül állandó és egyenlő sebességgel azonos irányba forgatva, az egyenesek metszéspontjai a C0C1P0 háromszög köré írható kört járják be. Tegyük fel, hogy az egyenesek 360∘-os elforgatásához n időegységre van szükség, és tekintsük csak azokat a helyzeteket, amelyek a forgatás kezdete után k időegységgel keletkeznek (k=1,2,...,n-1) akkor a megfelelő metszéspontokat Pk-val jelölve, a kapott P0P1...Pn-1 sokszög szabályos n-szö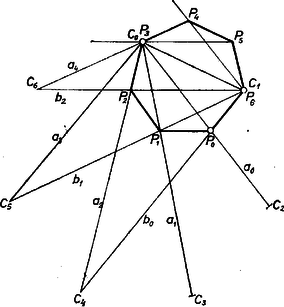g.
 

 

Mivel a P0,P1,...,Pn-1 pontokról már tudjuk, hogy egy körön vannak, csak azt kell belátnunk, hogy az általuk meghatározott ívek egyenlőek, ami viszont azért igaz, mert például C0-ból nézve őket, rendre egyenlő szög alatt látszanak. Alkalmazzuk ezt az állítást a vizsgált C0C1...C6 hétszögben, C0, C1 mellé P0 szerepére M-et választva kapjuk, hogy N a következő csúcs, vagy is P1 lesz; P2 a C0C4, C1C6 egyenesek metszéspontja, P3 a C0C3 és C0C1 közös pontja, azaz maga C0, P4 és P5 megrajzolásához a C0, C1-beli érintők is kellenének, de végül P6 nem lesz más, mint C1. Tehát C1C6 azonos P2P6-tal, ami párhuzamos P0P1-gyel, azaz MN-nel.