Kezdőlap


Feladat:	F.1969	Korcsoport: 18-	Nehézségi fok: -
Füzet:	1975/november, 123 - 124. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenletek, Egyenesek egyenlete, Parabola egyenlete, Parabola, mint kúpszelet, Feladat
Hivatkozás(ok):	Feladatok: 1975/január: F.1969

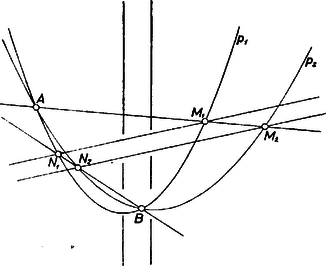
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az állítást a koordinátageometria eljárásaival bizonyítjuk. Válasszuk koordináta-rendszerünk tengelyeit és hosszúságegységét úgy, hogy $p_{1}$ egyenlete a következő legyen:

\begin{matrix} y = x^{2} . \end{matrix}

(1)

Ekkor

p_{2}

egyenlete, a szimmetriatengelyek párhuzamossága alapján

\begin{matrix} y = q x^{2} + r x + s, \end{matrix}

(2)

alakú, ahol a

q (\neq 0)

állandót

p_{2}

(geometriai) paramétere határozza meg, az

r

s

állandókat pedig

p_{2}

-nek

p_{1}

-hez képest elfoglalt helyzete.

A

B

pontok

x_{A}

x_{B}

abszcisszái az

(1)

(2)

rendszerből a

\begin{matrix} (q - 1) x^{2} + r x + s = 0 \end{matrix}

(3)

egyenlet gyökei, ahol ‐ mivel

A

és

B

léteznek és különbözők ‐

\begin{matrix} q - 1 \neq 0, r^{2} - 4 (q - 1) s > 0, \end{matrix}

és ekkor a gyökök és az együtthatók közti ismert összefüggés alapján

\begin{matrix} (q - 1) (x_{A} + x_{B}) = - r . \end{matrix}

(4)

Jelöljük még az

M_{i}

N_{i}

pont

(i = 1,2)

abszcisszáját rendre

m_{i}

-vel,

n_{i}

-vel, így a

p_{2}

húregyeneseként az

M_{2} N_{2}

egyenes iránytangense

\begin{matrix} \frac{(g m_{2}^{2} + r m_{2} + s) - (q n_{2}^{2} + r n_{2} + s)}{m_{2} - n_{2}} = q (m_{2} + n_{2}) + r . \end{matrix}

(5)

Ebből úgy kapjuk

M_{1} N_{1}

-nek, a

p_{1}

húregyenesének iránytangensét, hogy a

2

-es indexeket

1

-esre cseréljük, másrészt

(2)

és

(1)

összehasonlítása alapján

q = 1

-et és

r = s = 0

-t írunk:

\begin{matrix} m_{1} + n_{1}, \end{matrix}

(6)

és a feltevések alapján azt kell megmutatnunk, hogy e két iránytangensből képzett

\begin{matrix} D = g (m_{2} + n_{2}) + r - (m_{1} + n_{1}) \end{matrix}

(7)

különbség értéke

0

.
Hasonlóan számíthatjuk ki más szereplő húrok iránytangensét is: az

A M_{1}

A M_{2}

egyenesek meredekségét például úgy kaphatjuk meg a fenti eredményből, ha

N_{1}

, illetve

N_{2}

szerepét az

A

pontnak adjuk át, vagyis

(6)

-ban

n_{1}

, illetve

(5)

-ben

n_{2}

helyére

x_{A}

-t írunk. Ez a két meredekség egyenlő, hiszen az

A

M_{1}

M_{2}

pontok egy egyenesen vannak, tehát a különbségük

0

\begin{matrix} g (m_{2} + x_{A}) + r - (m_{1} + x_{A}) = 0. \end{matrix}

(8)

Ugyanígy,

B

-t véve

M_{1}

és

M_{2}

helyére, az egybeeső

B N_{2}

és

B N_{1}

egyenesek iránytangenseinek egyenlőségéből

\begin{matrix} g (x_{B} + n_{2}) + r - (x_{B} + n_{1}) = 0. \end{matrix}

(9)

Vonjuk le

(7)

-ből

(8)

-at és

(9)

-et

\begin{matrix} D = - (q - 1) (x_{A} + x_{B}) - r, \end{matrix}

erről pedig

(4)

alapján látjuk, hogy értéke valóban

0

. Ezzel az állítást bebizonyítottuk.

Megjegyzés. A

(4)

összefüggéssel látszólag nem használtuk ki teljes mértékben, hogy

x_{A}

és

x_{B}

(3)

egyenlet gyökei, ti. szorzatukról fel sem írtuk a

(g - 1) x_{A} x_{B} = s

összefüggést, ami a

(3)

-mal együtt egyértelmű lenne a gyököknek képlettel való felírásával. Azonban

(8)

és

(9)

megállapításában szóban használtuk fel, hogy pl.

A

játszhatja

N_{2}

és

N_{1}

szerepét.