Feladat: F.1964 Korcsoport: 18- Nehézségi fok: -
Megoldó(k):  Kiss Katalin 
Füzet: 1975/október, 64 - 66. oldal  PDF  |  MathML 
Témakör(ök): Terület, felszín, Térfogat, Térgeometria alapjai, Feladat
Hivatkozás(ok):Feladatok: 1974/december: F.1964

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a vizsgált testet K-val, a feladatban utoljára említett két csúcsát A-val, B-vel. Mivel 3 egységnyi él csak ezekből indul, a belőlük induló 3 egységnyi él az őket összekötő AB szakasz. Ez az él a K-t önmagába vivő tetszőleges tükrözéssel önmagába megy át, hiszen K-nak nincs más, vele egyenlő hosszú éle.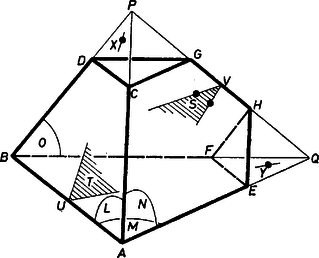

 

 

Jelöljük az AB élt alkotó lapokat L-lel, M-mel. Ezek a K-t önmagába vivő tükrözéskor vagy önmagukba vagy egymásba mennek át. Ha egy tükrözés K-t önmagába viszi, és az L,M lapokat felcseréli, akkor a tükrözés síkja átmegy AB-n, elválasztja egymástól az L,M lapokat és felezi a lapok síkja által alkotott szöget. Ez a sík tehát egyértelműen meghatározott, jelöljük S-sel. ‐ Ha pedig egy tükrözés K-t, L-et, M-et önmagába viszi, akkor síkja csak AB felező merőlegese lehet, jelöljük ezt T-vel. K-t tehát csak az S-re, T-re vonatkozó tükrözések vihetik önmagába, és mivel K-nak két szimmetriasíkja van, ezek a tükrözések önmagába is viszik át a K-t.
Az A-ból, B-ből induló, AB-től különböző élek hossza 2 egység. Mivel A-n és B-n kívül nincs K-nak olyan csúcsa, melyből két db 2 egységnyi él indulna, azért ezeknek az éleknek a másik végpontjuk nem lehet azonos. Jelöljük L-nek A-val, B-vel szomszédos csúcsait C-vel, D-vel, ezek S-re vonatkozó tükörképét E-vel, F-fel. Ekkor AC=AE=BD=BE=2.
Mivel a T-re vonatkozó tükrözés C-t és D-t felcseréli, azért CD⊥T, azaz CD||AB, vagyis az ABCD idom szimmetrikus trapéz, ABFE is az, CDFE pedig téglalap. Mivel A-hoz, B-hez más él nem csatlakozik, K-nak az ACE, BDF síkokban is van egy-egy lapja, jelöljük ezeket N-nel, O-val. Az előírás szerint K-nak 8 csúcsa van, közülük már említettünk 6-ot, ezeken kívül még 2 csúcs van. Be fogjuk látni, hogy ezek N-nek is, O-nak is csúcsai.
Először megmutatjuk, hogy L azonos az ABCD trapézzal. Ha ugyanis L-nek volna még egy X csúcsa, akkor L konvexitása miatt az csak CD-nek AB-t nem tartalmazó oldalán lehetne. Így X-nek S-re vonatkozó Y tükörképe ‐ az M lapban ‐ különbözne X-től: ez volna K nyolcadik csúcsa. K konvexitása miatt XY éle volna K-nak, és mivel más csúcsa már nincs K-nak, azért CE és DF is él volna. Ámde ekkor XY=CE=DF=1 volna, hiszen K még nem említett élei mind 1 egységnyiek. Emiatt a CDX, EFY síkok párhuzamosak volnának, ami nem lehet, hiszen ezek az egymáshoz AB-ben csatlakozó L,M lapok síkjai. Ezzel beláttuk, hogy L azonos az ABDC trapézzal, tehát CD éle a K-nak: CD=1.
Így az AC,BD egyenesek CD-nek AB-vel ellentétes oldalán metszik egymást, jelöljük a metszéspontjukat P-vel, P-nek S-re vonatkozó tükörképét Q-val. A PCD, PAB háromszögek hasonlóak, hasonlósági arányuk: 1:3, tehát AC=2 miatt PC=PD=1, vagyis a PCD, PAB háromszögek szabályosak, és szabályosak a QEF,QAB háromszögek is.
Jelöljük az AB,PQ szakaszok felezőpontját U-val, V-vel. Az S-re, T-re vonatkozó tükrözést egymás után végrehajtva az UV egyenesre való tükrözést (vagyis az egyenes körüli 180∘-os forgatást) kapjuk, feltevésünk szerint K-t ez a transzformáció is önmagába viszi. Mivel az eddig említett 6 csúcs halmaza S-re is, T-re is szimmetrikus, ilyennek kell lennie a még meg nem nevezett 2 csúcs halmazának is. A 2 csúcs által meghatározott szakasz tehát S-re is, T-re is, így az UV egyenesre nézve is szimmetrikus. K konvexitása miatt ez a szakasz nem lehet az UV egyenesen, tehát a hiányzó pontok egyike sem lehet az UV egyenesen.
Az S-re vonatkozó tükrözés AC-t AE-be viszi, tehát ez a tükrözés N-et önmagába viszi. N nem lehet azonos az ACE háromszöggel, hiszen ekkor K-nak csak az A,B,C,D,E,F pontok lehetnének a csúcsai. Jelöljük N-nek C-vel szomszédos (A-tól különböző) csúcsát G-vel, a K nyolcadik csúcsát H-val. Ha G az S-en van, akkor különböznie kell V-től, mert csak így nincs rajta a T-n is. Ekkor H a G-nek T-re vonatkozó tükörképe. Ámde ezek a pontok csak a CDFE téglalap AB-vel ellentétes oldalán lehetnének, így CD=1 miatt GH<1 volna, ami nem lehet.
G tehát nem lehet rajta S-en, így S-re vonatkozó H tükörképe is csúcsa N-nek. Mivel K-nak további csúcsa nincs, a G,H pontok rajta vannak T-n, és így a PQ szakaszon is. Ekkor CG=CP=1,AP=AQ=3 miatt a CPG háromszög hasonló az APQ háromszöghöz, és PG=13PQ. Ugyanennyi a HQ szakasz is, tehát GH is harmada PQ-nak. Mivel GH éle K-nak, GH=1, vagyis PQ=3, az ABPQ tetraéder szabályos.
Könnyen látható, hogy az így egyértelműen kapott testnek megvannak a kívánt tulajdonságai. Térfogata az ABPQ tetraéder térfogatának (1-227)-szerese, tehát
VK=(1-227)924=2,946térfogategység.
Felszíne pedig az egységnyi oldalú szabályos háromszög területének
 


2{1+(32-1)+(32-2)}=32-szerese, azaz FK=83=13,86 területegység.
 
 Kiss Katalin (Budapest, Dózsa Gy. Gimn., III. o. t.)