Kezdőlap


Feladat:	F.1963	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Jakab Tibor , Jónás Béla , Kiss Sándor , Krausz Tamás , Krisztin Tibor , Márkus Gábor , Münnich Ákos , Nagy János , Papp László Dezső , Seress Ákos , Soukup Lajos
Füzet:	1975/november, 119 - 122. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenletek, Két pont távolsága, szakasz hosszúsága, Kör egyenlete, Diszkusszió, Síkgeometriai szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 1974/december: F.1963

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A szerkesztést a derékszögű koordináta-rendszerben fogjuk elvégezni. Az adott egyenesek közül $e_{1}$ -nek az $x$ tengely szerepét adjuk, $e_{3}$ -nak az $y$ tengelyét, ekkor $e_{2}$ és $e_{4}$ a síknegyedek felezői; vegyük az $e_{1}$ -et $e_{2}$ -be vivő $45^{\circ}$ -os elfordulás irányát pozitívnak, ekkor $e_{2}$ az $y = x$ egyenletű egyenes, $e_{4}$ egyenlete pedig $y = - x$ . Jelöljük a szerkesztendő $k$ kör sugarát $r$ -rel, $C$ középpontjának koordinátáit $u$ -val, $v$ -vel.
A tengelyekből kimetszett húrok hosszára

\begin{matrix} h_{1} = a = 2 \sqrt[]{r^{2} - v^{2}}, h_{3} = b = 2 \sqrt[]{r^{2} - u^{2}}, \end{matrix}

tehát

\begin{matrix} v^{2} = r^{2} - \frac{a^{2}}{4}, u^{2} = r^{2} - \frac{b^{2}}{4}, r^{2} = \frac{u^{2} + v^{2}}{2} + \frac{a^{2} + b^{2}}{8}, \end{matrix}

(1)

és így

k

egyenlete,

r

kiküszöbölésével

\begin{matrix} {(x - u)}^{2} + {(y - v)}^{2} - r^{2} = (x^{2} + y^{2}) - 2 (u x + v y) + \frac{u^{2} + v^{2}}{2} - \frac{a^{2} + b^{2}}{8} = 0. \end{matrix}

(2)

Innen

y = x

helyettesítéssel azt az egyenletet kapjuk, amelyet a

h_{2}

húr végpontjaihoz tartozó abszcisszák elégítenek ki:

\begin{matrix} x^{2} - (u + v) x + \frac{u^{2} + v^{2}}{4} - \frac{a^{2} + b^{2}}{16} = 0. \end{matrix}

Ebből elég felírnunk a két gyök (

x_{1}

és

x_{2}

) különbségének abszolút értékét, mert azt

(cos 45^{\circ})

-kal osztva, mindjárt megkapjuk a

h_{2}

húr hosszát. Mivel

x^{2}

együtthatója

1

, azért

| x_{2} - x_{1} |

-et a

D

díszkrimináns négyzetgyöke adja. Ehhez

\begin{matrix} D = {(u + v)}^{2} - (u^{2} + v^{2}) + \frac{a^{2} + b^{2}}{4} = 2 u v + \frac{a^{2} + b^{2}}{4}, \\ h_{2} = \sqrt[]{2} \cdot | x_{2} - x_{1} | = \sqrt[]{2 D} = \sqrt[]{4 u v + \frac{a^{2} + b^{2}}{2}} . & (3) \end{matrix}

Hasonlóan,

h_{4}

céljára

(2)

-be

y = - x

-et írva,

\begin{matrix} x^{2} - (u - v) x + \frac{u^{2} + v^{2}}{4} - \frac{a^{2} + b^{2}}{16} = 0, \\ h_{4} = \sqrt[]{\frac{a^{2} + b^{2}}{2} - 4 u v} . & (4) \end{matrix}

Behelyettesítve

(3)

-at és

(4)

-et a

h_{4} = 3 h_{2}

követelménybe, kellő alakítással

\begin{matrix} 4 (1^{2} + 3^{2}) u v = (1^{2} - 3^{2}) \frac{a^{2} + b^{2}}{2}, u v = - \frac{a^{2} + b^{2}}{10} . \end{matrix}

(5)

Ez az

(1)

-ből adódó

\begin{matrix} u^{2} - v^{2} = \frac{a^{2} - b^{2}}{4} \end{matrix}

(6)

egyenlettel együtt rendszert alkot

u

és

v

meghatározására.
Látjuk

(5)

-ből, hogy

u

és

v

ellentett előjelűek lesznek, tehát

C

a II. vagy a IV. síknegyedben van. Helyesebben: ha van megoldás, akkor mindegyikben, hiszen az origóra való tükrözés az adott egyeneseket önmagukba viszi át, tehát

k

-val együtt

O

-ra való tükörképe is megoldás. Elég tehát megszerkesztenünk azt a

C

középpontot, melyre

u < 0

és

v > 0

.
Kiszámítjuk

u^{2}

-et és

v^{2}

-et.

(5)

-ből

v

-t

(6)

-ba helyettesítve

\begin{matrix} u^{4} - \frac{a^{2} - b^{2}}{4} u^{2} - {(\frac{a^{2} + b^{2}}{10})}^{2} = 0, \end{matrix}

és mivel innen

u^{2}

kisebbik értéke negatív, (hiszen a két érték szorzata negatív), azért egyértelműen

\begin{matrix} {\begin{matrix} u^{2} = \frac{a^{2} - b^{2}}{8} + \sqrt[]{{(\frac{a^{2} - b^{2}}{8})}^{2} + {(\frac{a^{2} + b^{2}}{10})}^{2}} (> 0), & (7) \\ v^{2} = \frac{b^{2} - a^{2}}{8} + \sqrt[]{{(\frac{a^{2} - b^{2}}{8})}^{2} + {(\frac{a^{2} + b^{2}}{10})}^{2}} (> 0) . \end{matrix} \end{matrix}

Innen is, de már

(5)

(6)

-ból is látjuk, hogy

| u |

és

v

nagyságviszonya ugyanaz, mint

a

és

b

nagyságviszonya, továbbá

a

és

b

cseréjével

u^{2}

és

v^{2}

értéke csupán fölcserélődik. Ezek alapján szabad a szerkesztést úgy leírnunk, mintha

a \geq b

volna.

(7)

-ben a négyzetgyökjel alatt az adott

a

b

szakaszoknak

4

-edfokú kifejezése áll, ami egyben két négyzet összege. Megszerkeszthetnénk a négyzetgyököt és még

u^{2}

-et,

v^{2}

-et is, ha előzőleg szakaszokként állítanánk elő az

\begin{matrix} \frac{a^{2} - b^{2}}{8} és \frac{a^{2} + b^{2}}{10} \end{matrix}

(8)

kifejezéseket (amelyek elsődlegesen egy-egy területet jelentenek).
Egy

P Q = x

szakaszhoz

x^{2}

hosszúságú szakasz szerkesztése (többek között) a magasságával kettévágott derékszögű háromszög arányos szakaszainak felhasználásával lehetséges, amennyiben egy tetszőleges szakaszt hosszúságegységnek nyilvánítunk.

P Q

-ra merőlegesen felmérjük

P R = 1

-et, a

P R

egyenesből előbb a

Q R

szakasz felező merőlegesével kimetsszük

S

-et, majd az

S

körüli

S R

sugarú körrel

T

-t, ekkor

P T = P Q^{2} : P R = P Q^{2} = x^{2}

(1. ábra).

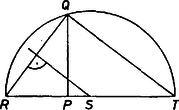1. ábra

Az ábra alapján világos, hogy megfordítva hogyan kapjuk az

1 = P R

és

x^{2} = P T

szakaszokból a

P Q = x

szakaszt.
Nem kell ezt az eljárást

a

-val és

b

-vel kezdenünk, mert a

(8)

kifejezések négyzetgyökét rövidebben kapjuk az alábbiak szerint. Szerkesszünk

D E F

derékszögű háromszöget,

D E = a

átfogóval,

D F = b

befogóval (2. ábra), így a

\begin{matrix} \sqrt[]{\frac{a^{2} - b^{2}}{8}} = \frac{1}{4} \sqrt[]{2 (a^{2} - b^{2})} \end{matrix}

szakaszt megadja az

E F

befogó mint oldal fölé szerkesztett négyzet átlójának

1 / 4

része,

E H

. ‐ Szerkesszünk másrészt

D E G

derékszögű háromszöget

D E = a

és

D G = b

befogókkal, és az

E G

átfogó fölé szerkesztett négyzet oldalait osszuk

3 - 3

egyenlő részre.

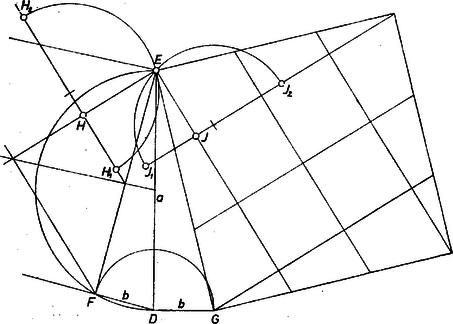2. ábra

Könnyű belátni, hogy az ábra szerinti

3 + 3

összekötő szakasz olyan részekre osztja a négyzetet, melyekből

10

egybevágó négyzet állítható össze, tehát egy kis négyzet oldala

\begin{matrix} E J = \sqrt[]{\frac{a^{2} + b^{2}}{10}} . \end{matrix}

Ezek alapján az

1.

ábrán bemutatott szerkesztést

x

helyén

E H

-ra és

E J

-re alkalmazva ‐ egységnek vettük

H H_{1} = J J_{1} = D F

-et ‐, az

x^{2}

szerepében kapott

H H_{2}

és

J J_{2}

adják a

(8)

kifejezéseknek megfelelő szakaszokat.
Legyenek most a

K L M

derékszögű háromszög befogói

K L = J J_{2}

K M = H H_{2}

(3. ábra), messe az

M

körüli,

M K

sugarú kör az

L M

átfogót

V_{2}

-ben, meghosszabbítását

U_{2}

-ben, ekkor

L U_{2}

és

L V_{2}

(7)

szerint

u^{2}

-nek,

v^{2}

-nek megfelelő szakasz.

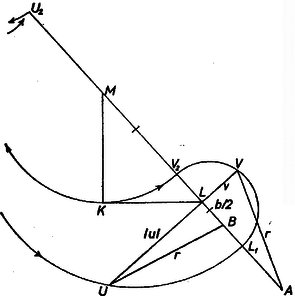3. ábra

Mérjük fel az átfogó

L

-en túli meghosszabbítására

L L_{1} = H H_{1}

-et, írjunk félköröket

L_{1} U_{2}

és

L_{1} V_{2}

mint átmérő fölé és messük ezeket az

L

-ben emelt merőlegessel

U

-ban,

V

-ben, ekkor

L U = | u |

és

L V = v

a keresett

k

kör

C

középpontjának koordinátái. Végül mérjük fel

L L_{1}

-re

L A = a / 2

-t,

L B = b / 2

-t, ekkor

V A = U B = r

k

-kör sugara. ‐ Mindezek alapján az eredményt a 4. ábra mutatja.

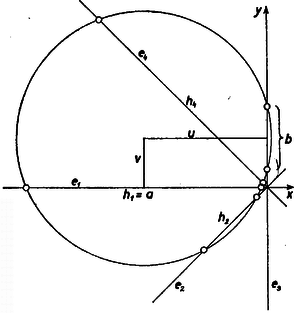4. ábra

A végzett szerkesztési lépések mindig egyértelműen végrehajthatók voltak.
A szerkesztés helyességének bizonyítását hely hiányában az olvasóra kell hagynunk.
Megjegyzések. 1. Egyszerűsíthető a szerkesztés, h a hosszúságegységnek magát

H E

-t vesszük; ekkora 2. ábrán

H_{1}

H_{2}

elmarad.
2. Kézenfekvő lenne a

2.

ábrán

E J

szerkesztését alkalmi fogásnak minősíteni, szemben

E H

nyilvánvaló szerkesztésével. Pedig ‐ ha a

h_{4} : h_{2} = 3 : 1

aránypár adott értékétől eltekintünk ‐

E J

szerkesztése mindig alkalmazható, amíg

h_{4} : h_{2} = λ

egész szám, és akkor is, ha

λ

racionális szám. Azon múlik ez, hogy a négyzetnek

(λ^{2} + 1)

számú egybevágó négyzetre való darabolását végezzük így.^{$^{*}$} Ezzel szemben

E H = (a^{2} - b^{2}) / 8 = (a^{2} - b^{2}) / (3^{2} - 1^{2})

szerkesztése alkalmi fogás, a

3^{2} - 1^{2} = 8

speciális értékre támaszkodik; általában négyzetnek

(λ^{2} - 1)

számú egybevágó négyzetre osztása nehézkesebb.

^{$^{*}$}Lásd 1142. gyakorlatunk megoldását K. M. L. 36. (1968) 117. old. Egyéb efféle darabolásokra vonatkozóan lásd az 50. kötet 3. számához mellékelt Tárgymutató X. oldalát.