Kezdőlap


Feladat:	F.1958	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Hanák L. , Krisztián T. , Soukup L.
Füzet:	1975/május, 206 - 207. oldal		PDF \| MathML
Témakör(ök):	Kocka, Mértani helyek, Térgeometria alapjai, Feladat
Hivatkozás(ok):	Feladatok: 1974/november: F.1958

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a körlemezt $k$ -val, középpontját $K$ -val, sugarát $r$ -rel a szóban forgó szöglet csúcsát $O$ -val, határoló síkjait rendre $S_{1}$ -gyel, $S_{2}$ -vel, $S_{3}$ -mal, $k$ síkját $S$ -sel, $k$ -nak $S_{i}$ -n levő érintési pontját $E_{i}$ -vel, $K$ -nak $S_{i}$ -n levő vetületét $K_{i}$ -vel, az $O$ -n átmenő, $S_{i}$ -re merőleges egyenest $e_{i}$ -vel $(i = 1, 2, 3)$ , és az $O$ -n átmenő, $S$ -re merőleges egyenest $e$ -vel. Mérjünk fel $O$ -ból $e$ -re valamelyik irányban $r$ -t, a kapott végpontot jelöljük $R$ -rel. Fektessünk $R$ -en át $S_{i}$ -vel párhuzamos síkot, messe ez $e_{i}$ -t $R_{i}$ -ben ( $i = 1$ , $2$ , $3$ ; lásd az 1. ábrát).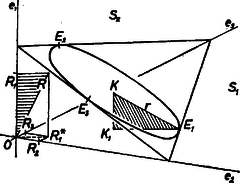

1. ábra

A következő megállapítások az

i = 1, 2, 3

értékek mindegyikére érvényesek. Mivel

k

érinti az

S_{i}

síkot,

S

és

S_{i}

különbözőek, emiatt

K_{i}

különbözik

K

-tól és

R_{i}

különbözik

R

-től. Ha

S ⊥ S_{i}

, akkor

K_{i}

, azonos

E_{i}

-vel, és

R_{i}

azonos

O

-val. Különben a

K

E_{i}

K_{i}

és az

R

O

R_{i}

pontok valódi háromszögeket határoznak meg. Ezekben

K_{i}

-nél, illetve

R_{i}

-nél derékszög van, és az elsőnek

E_{i}

-nél levő szöge egyenlő a másodiknak

O

-nál levő szögével, hiszen e szögek szárai merőlegesek, és mindkét szög hegyesszög. Emiatt

\begin{matrix} O R_{i} = E_{i} K_{i} és O R_{i}^{2} + R_{i} R^{2} = E_{i} K_{i}^{2} + K_{i} K^{2} = r^{2} . \end{matrix}

(1)

Könnyen látható, hogy (1) az

S ⊥ S_{i}

, esetben is érvényes, hiszen ekkor

O R_{i} = E_{i} K_{i} = 0

.
Jelöljük

R

-nek

S_{1}

-en levő vetületét

R_{1}^{*}

-gal, ekkor

\begin{matrix} O R^{2} = O R_{1}^{* 2} + R_{1}^{*} R^{2} = O R_{2}^{2} + O R_{3}^{2} + O R_{1}^{2} . \end{matrix}

(2)

Hasonlóan kapjuk, hogy

\begin{matrix} O K^{2} = K K_{1}^{2} + K K_{2}^{2} + K K_{3}^{2}, \end{matrix}

amiből (1) és (2) alapján

\begin{matrix} O K^{2} = (r^{2} - E_{1} K_{1}^{2}) + (r^{2} - E_{2} K_{2}^{2}) + (r^{2} - E_{3} K_{3}^{2}) = \\ = 3 r^{2} - (O R_{1}^{2} + O R_{2}^{2} + O R_{3}^{2}) = 3 r^{2} - O R^{2} = 2 r^{2} . \end{matrix}

Ha tehát

K

a mértani helyhez tartozik, akkor

\begin{matrix} O K^{2} = 2 r^{2}, 0 < K K_{1}, K K_{2}, K K_{3} \leq r . \end{matrix}

(3)

Ezek szerint

K

rajta van az

O

középpontú,

\sqrt[]{2} r

sugarú

G

gömbön, de az

S_{1}

S_{2}

S_{3}

síkoktól mért távolsága nem lehet

r

-nél nagyobb. Az utóbbi feltétel arra az

O

centrumú,

2 r

élű

K

kocka pontjaira teljesül, amelynek lapjai rendre párhuzamosak

S_{i}

-vel, így a

G

-n levő pontok közül el kell hagynunk a

K

-n kívül levőket, valamint az

S_{i}

síkok pontjait. Jelöljük a visszamaradó pontok halmazát

G_{0}

-lal, megmutatjuk, hogy ennek minden pontja a vizsgált mértani helyhez tartozik (2. ábra).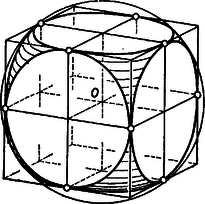

2. ábra

Legyen

K

tetszőleges pont a térben, melyre teljesül (3), ahol

K_{i}

K

-nak az

S_{i}

-n levő vetülete

(i = 1, 2, 3)

. Tekintsük az

S_{l}

S_{2}

S_{3}

síkok által határolt 8 térrész közül azt a térnyolcadot, amelyik tartalmazza

K

-t. Mérjük fel az

e_{i}

egyenesre ebben a térnyolcadban az

\begin{matrix} O R_{i} = \sqrt[]{r^{2} - K_{i} K^{2}} \end{matrix}

szakaszokat, és húzzunk az

R_{i}

ponton át

S_{i}

-vel párhuzamos síkot

(i = 1, 2, 3)

. Jelöljük a három új sík metszéspontját

R

-rel, erre (3) miatt

\begin{matrix} O R^{2} = O R_{1}^{2} + O R_{2}^{2} + O R_{3}^{2} = r^{2}, \end{matrix}

tehát

R R_{1} = K K_{1}, R R_{2} = K K_{2}, R R_{3} = K K_{3} .

Fektessünk át

K

-n

O R

-re merőleges

S

síkot. A következő megállapításaink ismét érvényesek lesznek az

i = 1, 2, 3

értékek mindegyikére. Mivel

K K_{i} > 0

, és

O R_{i} < r

, vagyis

R_{i}

különbözik

R

-től, tehát

S

nem lehet párhuzamos

S_{i}

-vel. Jelöljük

S

és

S_{i}

metszésvonalát

m_{i}

-vel,

K

-nak

m_{i}

-n levő merőleges vetületét

E_{i}

-vel. Mivel

O R ⊥ K E_{i}

, és

R R_{i} = K K_{i}

, azért az

O R R_{i}

E_{i} K K_{i}

háromszögek ismét egybevágóak (esetleg bennük egyszerre

O

R_{i}

-vel,

E_{i}

K_{i}

-vel azonos), tehát

\begin{matrix} K E_{i} = O R = r, \end{matrix}

vagyis az

S

síkban

K

körül

r

sugárral rajzolt

k

kör érinti az

m

egyenest.

K

tehát valóban a mértani helyhez tartozik.

Megjegyzés. Megoldásunk második felében elég volt

k

-nak egy megfelelő állását megtalálnunk. Hogy ennek megfelelően csak egyet adtunk meg, az még nem jelenti azt, hogy csak egy van. Általában a megfelelő körök száma négy, kivéve, ha

K

K

kocka, felületén van, ekkor a helyzetek száma csak kettő.