Kezdőlap


Feladat:	F.1957	Korcsoport: 18-	Nehézségi fok: -
Füzet:	1975/november, 112 - 115. oldal		PDF \| MathML
Témakör(ök):	Geometriai transzformációk, Műveletek helyvektorok koordinátáival, Egyenesek egyenlete, Koordináta-geometria, Feladat
Hivatkozás(ok):	Feladatok: 1974/november: F.1957

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. 1. A $P P'$ egyenes iránytangense az adott összefüggések felhasználásával

\begin{matrix} m = \frac{b' - b}{a' - a} = \frac{0, 8 a - 1, 6 b}{- 0, 4 a + 0, 8 b} = - \frac{0, 8}{0, 4} \cdot \frac{a - 2 b}{a - 2 b} = - 2, \end{matrix}

állandó, hacsak a nevezőre teljesül

\begin{matrix} a' - a = - 0, 4 (a - 2 b) \neq 0. \end{matrix}

Ez a követelmény első alakjában azt jelenti, hogy

P'

és

P

abszcisszái különbözők, második alakjában pedig azt, hogy

a - 2 b \neq 0

, másképpen

a \neq 2 b

, vagyis

P

abszcisszája és ordinátája közt kizártunk egy első fokú kapcsolatot. Általában az

x = 2 y

, vagy

y = \frac{1}{2} x

kapcsolat a koordináta-rendszerben egy meghatározott

t

egyenest jelent, azt kaptuk tehát, hogy ha

P

nincs rajta

t

-n, akkor

P P'

iránytényezője

2

.
Ha viszont

a' - a = 0

, azaz

a' = a

és

a = 2 b

, vagyis

P

rajta van

t

-n, akkor

(1)

alapján

\begin{matrix} b' = 1, 6 b - 0, 6 b = b, \end{matrix}

vagyis

P'

azonos

P

-vel, hiszen mindkét koordinátájuk egyenlő. Ekkor pedig nincs értelme beszélni összekötő egyenesükről.
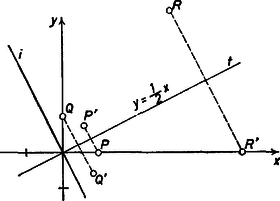
Ezek szerint a

P, P'

kapcsolatban ‐ nevezhetjük ponttranszformációnak ‐ valóban minden

P' \neq P

esetén a

P P'

egyenes párhuzamos az

m = - 2

iránytényezőjű egyenesek mindegyikével, speciálisan az origón átmenő,

y = - 2 x

egyenletű

i

egyenessel; az állítást bebizonyítottuk.
Például az

(1; 0)

pont leszármazottja

(0, 6; 0, 8)

, a

(0; 1)

ponté

(0,8; - 0, 6)

, a

(3; 4)

-é

(5; 0)

.
Azt is kaptuk, hogy az

(1)

egyenletrendszerrel leírt transzformációban az

y = \frac{1}{2} x

egyenletű

t

egyenes pontjai ‐ és csak ezek ‐ megkülönböztetett szerepet játszanak (hiszen más pontpárokra mindjárt

a' \neq a

), ezek önmaguk leszármazottai.
2. Keressük meg most a

P

-ből leszármaztatott

P'

-nek

P''

leszármazottját,

P

-nek második leszármazottját (a

t

-n levő

P

pont esetében

P' \equiv P

miatt természetesen

P'' \equiv P

).
Erre

\begin{matrix} a'' = 0, 6 a' + 0, 8 b' = 0, 6 (0, 6 a + 0, 8 b) + 0, 8 (0, 8 a - 0, 6 b) = a, \end{matrix}

és hasonlóan

b'' = b

, vagyis

P'

leszármazottja maga

P

.
Hozzávéve ehhez azt az észrevételt, hogy

t

merőleges

i

-re, vagyis minden

P, P'

pontpár összekötő egyenesére, kézenfekvő az a sejtés, hogy az

(1)

rendszer az

y = \frac{1}{2} x

egyenesre való tükrözés.

Ennek bizonyításához most már elég azt belátni, hogy a

P P'

szakasz felezőpontja a

t

-n van, vagyis hogy ordinátája feleakkora, mint az abszcisszája. Valóban:

\begin{matrix} \frac{a + a'}{2} & = 0, 8 a + 0, 4 b, \\ \frac{b + b'}{2} & = 0, 4 a + 0, 2 b, \end{matrix}

tehát sejtésünk igaz.

II. megoldás. Jelöljük a síknak a koordinátatengelyek pozitív irányába mutató egységvektorait

i

-vel,

j

-vel, az origót

O

-val, akkor a

P

pont helyvektora

\begin{matrix} r = \vec{O P} = a i + b j, \end{matrix}

és a

P

-hez rendelt

P'

pont helyvektora

\begin{matrix} r' = \vec{O P}' = a' i + b' j = (0, 6 a + 0, 8 b) i + (0, 8 a - 0, 6 b) j = a (0, 6 i + 0, 8 j) + b (0, 8 i - 0, 6 j) . \end{matrix}

Ebből

a = 1

b = 0

, illetve

a = 0

b = 1

helyettesítéssel kapjuk az

i

j

vektorok transzformált értékeit:

\begin{matrix} i' & = 0, 6 i + 0, 8 j & (2) \\ j' & = 0, 8 i - 0, 6 j, \end{matrix}

Ezeket az

r'

előállításába helyettesítve azt kapjuk, hogy

\begin{matrix} r' = a i' + b j' . \end{matrix}

Szavakkal elmondva ez azt jelenti, hogy a transzformált

P'

pontnak a transzformált

i'

j'

vektorok által meghatározott koordináta-rendszerben ugyanazok a koordinátái, mint az eredeti

P

pontnak az eredeti koordináta-rendszerben. Elég tehát azt megvizsgálnunk, hogyan kaphatjuk meg az

i'

j'

vektorokat az

i

j

vektorokból. Mivel a

(2)

-beli együtthatókra

\begin{matrix} 0, 6^{2} + 0, 8^{2} = 1, \end{matrix}

azért

i'

j'

is egységvektor. Másrészt

j'

i'

-ből negatív irányú

90^{\circ}

-os forgatással kapható meg, hiszen ez a forgatás

(0, 6 i)

-t

(- 0, 6 j)

-be,

(0, 8 j)

-t

(0, 8 i)

-be viszi, és e két vektor összegét az új vektorok összegébe viszi. Ha tehát megkeressük azt a

t

egyenest, amelyre

i

-t tükrözve

i'

-t kapjuk, biztosak lehetünk benne, hogy az

i

-ből pozitív irányú

90^{\circ}

-os forgatással kapható

j

-t erre a

t

-re tükrözve az

i'

-ből negatív irányú

90^{\circ}

-os forgatással kapható

j'

-t kapjuk.
Mivel

i'

is egységvektor,

t

valóban létezik, mégpedig

t

i

i'

vektorok által kijelölt szöget felező egyenes. A

t

-re való tükrözés az

i

vektor

a i

skalár-szorosát az

i

-nek

i'

képéből kapható

a i'

vektorba viszi,

b j

-t pedig

b j'

-be, és

(a i + b j)

-t

(a i' + b j')

-be, hiszen a vektorok összeadásához használt paralelogramma is tükröződik

t

-re. Ezzel beláttuk, hogy az

(1)

összefüggéssel megadott ponttranszformáció azonos a

t

egyenesre való tükrözéssel, ahol

t

az origón, és az

(1; 0)

(0, 6; 0, 8)

pontpár

(0, 8; 0, 4)

felezőpontján átmenő

\begin{matrix} y = \frac{1}{2} x \end{matrix}

egyenletű egyenes.

Megjegyzés. Ha

(1)

helyett az általános

\begin{matrix} a' = c_{11} a + c_{12} b; b' = c_{21} a + c_{22} b \end{matrix}

összefüggésből indultunk volna ki, az

\begin{matrix} i' & = c_{11} i + c_{21} j, \\ j' & = c_{12} i + c_{22} j \end{matrix}

vektorokat kaptuk volna, amelyek általában már nem merőlegesek, és nem egységvektorok. Az azonban továbbra is igaz marad, hogy tetszőleges

(i; j)

-beli pont képe a vele megegyező koordinátájú,

(i'; j')

-beli pont. A transzformációnk által adott képek tehát úgy viszonylanak az eredetihez, mint egy bizonyos összefüggésnek különböző koordináta-rendszerekben kapott képei.
Mondjuk, az

y = x^{2}

összefüggést ábrázoljuk különböző koordináta-rendszerekben, azaz tetszőleges

u

v

vektorok mellett megkeressük az

\begin{matrix} r = x u + x^{2} v \end{matrix}

helyvektorú pontok összeségét, midőn

x

befutja a valós számokat. Amíg az

(u; v)

vektorok merőlegesek, és egységnyi hosszúak, megválasztásuk nem szól bele a kapott pontokból kirajzolódó görbe alakjába. Ha azonban

(u; v)

tetszőleges vektorok, a vizsgált görbék alakja is megváltozik.
További általánosítást jelent, ha az origó helyzetét is megváltoztatjuk, amit az

\begin{matrix} a' & = c_{11} a + c_{12} b + c_{13} \\ b' & = c_{21} a + c_{22} b + c_{23} \end{matrix}

transzformációval érhetünk el. Jó szolgálatot tesznek ezek a transzformációk a bonyolultabb függvények alaki vizsgálatánál, segítségükkel ezeknek a tipizálása aránylag kényelmesen elvégezhető.
Külön említésre méltóak az

\begin{matrix} A x^{2} + B x y + C y^{2} + D x + E y + F = 0 \end{matrix}

egyenletű ún. másodrendű görbék, amelyekről e transzformációk segítségével lehet belátni, hogy valamennyiük kúpszelet, tehát a fenti egyenlet képe vagy ellipszis, vagy hiperbola, vagy parabola, vagy metsző egyenespár, vagy párhuzamos egyenespár, vagy egy egyenes, vagy egy pont, vagy üres halmaz (a kört e fölsorolásban az ellipszisekhez soroltuk).