Feladat:	F.1956	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Bagó Balázs ,  Bérczi Tamás ,  Binzberger Gábor ,  Bíró András ,  Böősi Imre ,  Csige Sándor ,  Fehér Zoltán ,  Gáti Tamás ,  Homonnay Géza ,  Horváth József (Hódmezővásárhely) ,  Hujter Mihály ,  Ivanyos Gábor ,  Jakab Tibor ,  Jónás Béla ,  Koltay Károly ,  Krausz Tamás ,  Krisztin Tibor ,  Kun Attila ,  Maczák János ,  Mikoss László ,  Papp László Dezső ,  Seress Ákos ,  Soukup Lajos ,  Sparing László ,  Stark Gusztáv ,  Strommer Pál ,  Szabó Kálmán (Miskolc) ,  Tokodi Jenő ,  Zelhofer Walter
Füzet:	1975/szeptember, 11 - 13. oldal		PDF  |  MathML
Témakör(ök):	Háromszögek hasonlósága, Trigonometrikus egyenlőtlenségek, Háromszögek nevezetes tételei, Szinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1974/november: F.1956

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. $\begin{array}{c}{\displaystyle \text{sin}\alpha \text{sin}\beta \le \text{sin}{}^2\frac{\gamma }{2}\mathrm{.}}\end{array}$ (1) I. megoldás. Tegyük föl, hogy az $AB$ szakaszon létezik a kérdéses $D$ pont, és jelöljük a $CD$ egyenesnek a háromszög köré írt $k$ körrel való második metszéspontját $E$-vel. Ekkor a föltevés szerint $\begin{array}{c}{\displaystyle AD\cdot DB=D{C}^2\mathrm{.}}\end{array}$ (2) Másrészt az $ADC$ és $EDB$ háromszögek hasonlók, mert $D$ a $k$ belsejében van, ezért $E$ ugyanazon oldalán van a $BC$ húrnak, mint $A$, tehát a két háromszögben a felsorolás szerinti első két‐két csúcsnál levő szögek páronként egyenlők. Így $\begin{array}{c}{\displaystyle \frac{AD}{DC}=\frac{ED}{DB}\mathrm{,}\text{azaz}AD\cdot DB=DC\cdot ED\mathrm{.}}\end{array}$ (3) A (2) és (3) egyenlőségekben 3‐3 tényező egyezik, így a negyedik tényezők is, ezért $\begin{array}{c}{\displaystyle ED=DC\mathrm{,}}\end{array}$ vagyis $E$ a $C$ csúcs tükörképe $D$-re. Eszerint $E$ a $k$-nak olyan pontja, mely $AB$-től akkora távolságban van, mint $C$; tehát $E$ és vele $D$ létezésének szükséges föltétele, hogy a $C$-n átmenő, $AB$-vel párhuzamos egyenesnek $AB$-re való $e$ tükörképe messe $k$-t. Ez a föltétel elegendő is, mert ha $E$ közös pontja az $e$-nek és a $k$-nak, akkor a $CE$ egyenes metszi $AB$-t, ezen $D$ metszéspontra $DE=DC$, és így a (2) szerint $D$ megfelel és $A$ és $B$ közé esik. Legyen a $C$-t nem tartalmazó $AB$ ívnek $AB$-től legtávolabbi pontja ‐ vagyis a felező pontja ‐ $F$, továbbá $C$ és $F$ vetülete $AB$-re $C\text{'}$, $F\text{'}$, ekkor a talált feltétel így írható: $\begin{array}{c}{\displaystyle CC\text{'}\leqq FF\text{'}\mathrm{.}}\end{array}$ (4) Válasszuk hosszegységnek körünk $2r$ átmérőjét, ekkor a szögek felhasználásával, és mivel $CF$ felezi $\gamma$-t: ${\displaystyle \begin{array}{c}\hfill {\displaystyle CC\text{'}=CB\text{sin}\beta =\left(2r\text{sin}\alpha \right)\text{sin}\beta =\text{sin}\alpha \text{sin}\beta \mathrm{,}}\hfill \\ \hfill {\displaystyle FF\text{'}=FB\text{sin}\frac{\gamma }{2}=\left(2r\text{sin}\frac{\gamma }{2}\right)\text{sin}\frac{\gamma }{2}=\text{sin}{}^2\frac{\gamma }{2}\mathrm{.}}\hfill \end{array}}$ Ezeket (4)-be helyettesítve a feltételünkkel ekvivalens (1)-et kapjuk.    Soukup Lajos (Budapest, I. László Gimn., III. o. t.)   Megjegyzés. Tompaszögű háromszögben ‐ amennyiben a tompaszög $C$-nél van ‐ (4) eleve teljesül, hiszen $CC\text{'}<r<FF\text{'}$. Ebből a bizonyított állításnál érdekesebb eredményt kapunk: ha $\gamma >{90}^{\circ }$ akkor $\text{sin}\alpha \text{sin}\beta <\text{sin}{}^2\gamma /2$   II. megoldás. Jelöljük a $DCA$, $DCB$ szöget rendre ${\gamma }_1$ gyel, ${\gamma }_2$-vel, ekkor a sinustétel alapján 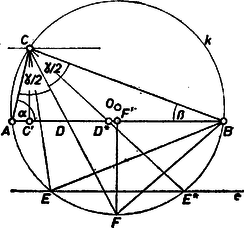$\begin{array}{c}{\displaystyle AD=CD\cdot \frac{\text{sin}{\gamma }_1}{\text{sin}\alpha }\mathrm{,}BD=CD\cdot \frac{\text{sin}{\gamma }_2}{\text{sin}\beta }\mathrm{.}}\end{array}$     Ezeket az $AD\cdot BD=C{D}^2$ követelménybe helyettesítve $\begin{array}{c}{\displaystyle AD\cdot BD=C{D}^2\frac{\text{sin}{\gamma }_1\text{sin}{\gamma }_2}{\text{sin}\alpha \text{sin}\beta }=C{D}^2\mathrm{,}}\end{array}$ vagyis az ezt kielégítő $D$ pont mellett a szögekre teljesül, hogy $\begin{array}{c}{\displaystyle \text{sin}{\gamma }_1\text{sin}{\gamma }_2=\text{sin}\alpha \text{sin}\beta \text{és}{\gamma }_1+{\gamma }_2=\gamma \mathrm{.}}\end{array}$ (5) Mármost ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{sin}{\gamma }_1\text{sin}{\gamma }_2=\frac{1}{2}\left[\text{cos}\left({\gamma }_1-{\gamma }_2\right)-\text{cos}\left({\gamma }_1+{\gamma }_2\right)\right]\leqq \frac{1}{2}\left[1-\text{cos}\gamma \right]=\text{sin}{}^2\frac{\gamma }{2}\mathrm{,}}\hfill \end{array}}$ ezt (5)-tel egybevetve (1)-et kapjuk. Ezzel beláttuk, hogy ha a mondott tulajdonságú $D$ pont létezik, akkor teljesül (1). Tegyük most fel, hogy a háromszög szögeire teljesül (1). Ekkor van olyan $\delta$ szög, amelyre $0\leqq \delta \leqq \pi$, és $\begin{array}{c}{\displaystyle \text{cos}\delta =2\text{sin}\alpha \text{sin}\beta +\text{cos}\gamma \mathrm{,}}\end{array}$ hiszen itt a jobb oldal értéke mindig legalább $-1$, és (1) teljesülése esetén $\begin{array}{c}{\displaystyle 2\text{sin}\alpha \text{sin}\beta +\text{cos}\gamma \leqq 2\text{sin}{}^2\frac{\gamma }{2}+\text{cos}\gamma =1.}\end{array}$ Mivel erre a $\delta$ szögre $\text{cos}\delta >\text{cos}\gamma$, és így $\delta <\gamma$, azért a $\begin{array}{c}{\displaystyle {\gamma }_1=\frac{\gamma -\delta }{2}\mathrm{,}{\gamma }_2=\frac{\gamma +\delta }{2}}\end{array}$ szögek pozitívak, és rájuk teljesül (5). A fenti gondolatmenet megfordításával viszont ebből azt kapjuk, hogy a ${\gamma }_1$, ${\gamma }_2$ szögekhez tartozó $D$ pontra $CD$ az $AD$, $BD$ szakaszok mértani közepe, (1) tehát valóban elégséges feltétele az ilyen $D$ pont létezésének.    Krausz Tamás (Debrecen, Fazekas M: Gimn., IV. o. t.)