| Feladat: | F.1950 | Korcsoport: 18- | Nehézségi fok: - |
| Füzet: | 1975/május, 204 - 205. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Háromszögek nevezetes tételei, Körök, Trapézok, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1974/október: F.1950 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Jelöljük a , átmérőjű kört rendre -val, -vel, és legyen egy, az előírásnak megfelelő, körüli kör . (Az utóbbi minden háromszögben lehetséges, hiszen és két különböző pontban metszik egymást.) Legyen a körpár egyik közös pontja , és tekintsük a egyenesnek -vel való, -től különböző metszéspontját. Azt mutatjuk meg, hogy rajta van -n. 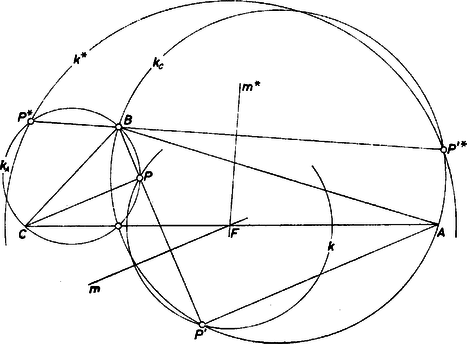 Thalész tétele alapján -re merőlegesen áll is, is, tehát és egy trapéz párhuzamos oldalai, pedig vagy átlója ennek vagy szára. (Az ábra -nak egy más, helyzetét is mutatja; és esetében átló, a és esetében szár az szerepe. Ha éppen -ben van, akkor -n -nak -beli érintője értendő, hasonlóan értendő , ha az -ban adódik, ezekben az esetekben derékszögű háromszög adódik a trapéz helyett.) Így az -en át -re állított merőleges a trapéznak középvonala, tehát merőlegesen felezi a szakaszt, hiszen ez is átlója vagy szára a trapéznak. Eszerint , a -n is rajta van, amint állítottuk. Így a , köröknek közös pontja, és a -n levő , pontpár megfelel a feladat állításának. A , körök -től különböző közös pontjához ugyanígy adódik párként -nek és -nak egy közös pontja. Csak azt kell még belátnunk, hogy és különbözők. Ez abból adódik, hogy a és egyenesek különbözők, mert egy egyenesnek nem lehet 3 közös pontja egy körrel. (Akkor is különböző és , ha átmegy -n, vagyis és egyike maga , hiszen pl. esetén -ként érintője veendő.) Azt is kaptuk, a feladat állításának kiegészítéséül, hogy a metszéspontpárok egyik eleme mindig -hoz, másika a -hez tartozik. Az pont és , középpontja az háromszög középháromszögének csúcsai, -vel kiegészítve paralelogrammát adnak. Ebből adódik, hogy sugarának nagyobbnak kell lennie -nél és kisebbnek kell lennie -nél. Ha a sugár egyenlő bármelyik mondott korláttal, akkor egyidejűen érinti és mindegyikét. A két ilyen érintkezési pont kivételével -nak minden pontja szerepelhet -ként (-ként), és -nek minden pontja adódik -ként (-ként). (Egyébként és szerepe nyilvánvalóan fölcserélhető.) |