Kezdőlap


Feladat:	F.1945	Korcsoport: 18-	Nehézségi fok: -
Füzet:	1975/február, 66 - 67. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Síkgeometriai számítások trigonometria nélkül háromszögekben, Szinusztétel alkalmazása, Koszinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1974/szeptember: F.1945

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A háromszögben szokásos jelölésekkel a föltevések és az állítás így írhatók:

\begin{matrix} A P = \frac{c}{4}, P B = \frac{3 c}{4}, B P C ∢ = \frac{β}{2}, illetve b = a + \frac{c}{2} . \end{matrix}

Mivel

P C B ∢ = 180^{\circ} - \frac{3 β}{2} > 0^{\circ}

, azért

β < 120^{\circ}

, azaz

B

-nél tompaszög is előfordulhat. Legyen

B

tükörképe a

C C_{1}

, magasságvonalára

B'

, ekkor a

B' P C

háromszög mindenképpen egyenlő szárú:

B' P = B' C = C B = a

. Ez

β = 90^{\circ}

esetén nyilvánvaló, különben pedig a külső szög tételéből következik; a

B' P C

háromszög

B'

-nél levő külső szöge

β < 90^{\circ}

és

β > 90^{\circ}

esetén egyaránt

β

, így mindig

B' C P ∢ = B' P C ∢ = β / 2

. Ezekből a

C B B'

egyenlő szárú háromszög alapja

\begin{matrix} B B' = \frac{3 c}{4} - a, illetve a - \frac{3 c}{4}, B C_{1} = | \frac{3 c}{8} - \frac{a}{2} |, \end{matrix}

és mindkét esetben

\begin{matrix} A C_{1} = c - \frac{B B'}{2} = \frac{5 c}{8} + \frac{a}{2}, illetve A C_{1} = c + \frac{B B'}{2} = \frac{5 c}{8} + \frac{a}{2} . \end{matrix}

Most már az

A C C_{1}

és

B C C_{1}

derékszögű háromszögekből

\begin{matrix} b^{2} = A C_{1}^{2} + C C_{1}^{2} = {(\frac{5 c + 4 a}{8})}^{2} + (C B^{2} - B C_{1}^{2}) = a^{2} + {(\frac{5 c + 4 a}{8})}^{2} - {(\frac{3 c - 4 a}{8})}^{2} = {(a + \frac{c}{2})}^{2}, \end{matrix}

és ez bizonyítja az állítást.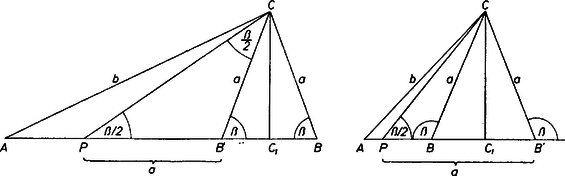

II. megoldás. A

P B C

háromszög

C

-nél levő szöge

180^{\circ} - \frac{3 β}{2}

, ezért a sinustétel és ismert azonosságok alapján

\begin{matrix} \frac{P B}{B C} = \frac{3 c}{4 a} = \frac{sin (180^{\circ} - \frac{3 β}{2})}{sin \frac{β}{2}} = \frac{sin \frac{3 β}{2}}{sin \frac{β}{2}} = 3 - 4 sin^{2} \frac{β}{2}, \\ cos β = 1 - 2 sin^{2} \frac{β}{2} = 1 + \frac{3 c}{8 a} - \frac{3}{2} = \frac{3 c - 4 a}{8 a} . \end{matrix}

Így pedig az

A B C

háromszögben a cosinustétel alapján ismét

\begin{matrix} b^{2} = a^{2} + c^{2} - 2 a c cos β = {(a + \frac{c}{2})}^{2} . \end{matrix}

Megjegyzés. Bizonyítható az állítás Stewart tétele alapján is, azt is felhasználva, hogy a

C B P

háromszöget a

B D

szögfelező úgy vágja ketté, hogy

B D P

rész egyenlő szárú háromszög,

C D B

rész pedig a felosztás előttihez hasonló háromszög.