Kezdőlap


Feladat:	F.1944	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Alexy M. , Bajza Auguszta , Balaskó A. , Baranyi A. , Bátki Zs. , Binzberger G. , Böősi I. , Csathó Beáta , Decsi I. , Dörgő M. , Felföldi J. , Jani G. , Jávor F. , Jónás B. , Kiss A. , Kiss E. , Knébel I. , Madocsi Zs. , Molnár Z. , Rochlitz I. , Schmidt J. , Seress Á. (II. o.) , Soukop Z. , Szabó Erzsébet , Szabó K. , Tornóci L. , Tóth K. , Tóth S. , Upor L. , Zelhofer W. (III. oszt.)
Füzet:	1975/február, 64 - 66. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Diszkusszió, Síkgeometriai szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 1974/szeptember: F.1944

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Az $A B C$ háromszög $A B$ -re merőleges területfelezőjét szerkesztjük azzal a feltevéssel, hogy az $M N$ szelőszakasz az $A B$ szakasz egy belső $M$ pontjából indul ki. A további két oldalról feltehetjük, hogy $C A > C B$ ‐ hiszen $C A = C B$ esetén nyilvánvalóan a $C T$ magasság a felező, a feladat érdektelen, ha pedig $C A < C B$ volna, úgy az $A$ , $B$ betűcserével teljesül feltevésünk.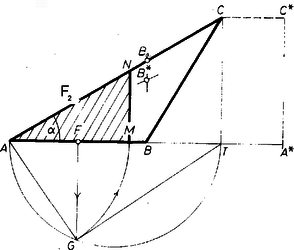

1. ábra

A kettévágott háromszög

A M N

része háromszög alakú, és a követelmény szerint

\begin{matrix} \frac{A M \cdot M N}{2} = \frac{A B \cdot T C}{4}, \end{matrix}

másrészt az

A M N

és

A T C

háromszögek hasonlósága alapján

\begin{matrix} \frac{A M}{M N} = \frac{A T}{T C}, \end{matrix}

és ezeket összeszorozva

\begin{matrix} A M^{2} = \frac{A B}{2} \cdot A T = A F \cdot A T, \end{matrix}

ahol

F

A B

alap felezőpontja. Eszerint

A M

az ismert

A F

és

A T

szakaszok mértani közepe.
Föltevésünk alapján

A T > A F

, és megfelel a következő szerkesztés. Legyen az

A T

átmérő fölötti Thalész‐körnek

F

fölötti (alatti) pontja

G

, ezt

A

körül az

A B

szakaszra ráforgatva kapjuk

M

-et.
A szerkesztés helyessége nyilvánvaló, és a szerkesztés mindaddig használható, amíg

\begin{matrix} A M = \sqrt[]{A F \cdot A T} \leq A B = 2 A F, \end{matrix}

másképpen, amíg

\begin{matrix} A T \leq 4 A F = 2 A B = A A^{*}, \end{matrix}

vagyis ha

T

A A^{*}

szakaszon van, ahol

A^{*}

A

tükörképe

B

-re. Amennyiben

A^{*}

éppen egybeesik

T

-vel, akkor

M

egybeesik

B

-vel,

A C

-nek

B

fölötti

B^{*}

pontjára

B B^{*} = T C / 2

, és az

A B B^{*}

háromszög területe valóban fele

A B C

területének.
2. A feladat szövege alapján szabadon választhatjuk, hogy a felezőegyenest melyik oldalra merőlegesen szerkesztjük. Ezért szerkesztésünk nyilvánvalóan minden hegyesszögű és derékszögű háromszögre érvényes, továbbá tompaszögű háromszög legnagyobb oldalára is, sőt még bizonyos

B ∢ > 90^{\circ}

esetekre is. Ezzel a feladatot megoldottuk.

Megjegyzések. 1. A talált szerkesztéshez nagyon hasonló eljárással

A T > A A^{*}

esetén is célhoz érünk. Messe a területfelező a

C B

C A

B T

szakaszt, valamint a

C

-n át

A B

-vel húzott párhuzamost rendre az

M

N

P

, illetve

Q

pontban (2. ábra).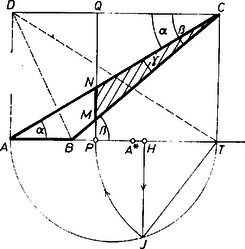

2. ábra

Ekkor háromszögünk két egyenlő területű része

A B M N

és

C M N

, és az ábra további jelöléseivel

\begin{matrix} C M N = \frac{1}{2} C M \cdot C N sin γ = \frac{C Q^{2} sin γ}{2 cos β cos α} = \frac{1}{2} C B A = \frac{1}{4} C B \cdot C A sin γ, \\ C Q = T P = \sqrt[]{\frac{1}{2} C B cos β \cdot C A cos α} = \sqrt[]{\frac{T B}{2} \cdot T A} = \sqrt[]{T H \cdot T A} = T J . \end{matrix}

Azt is látjuk innen az eredeti megoldás kellő átbetűzésével, hogy az

A B C

háromszög

A B

-re merőleges területfelezője azonos a

D B C

háromszög

D C

-re (

A B

-re) merőleges területfelezőjével, ahol

D

A

vetülete a

C

-n átmenő,

A B

-vel párhuzamos egyenesen.
2. Lényegében ugyanígy szerkeszthetjük az osztóvonal

N

végpontját is. Az 1. ábra esetében

\begin{matrix} A M N = \frac{1}{2} A N^{2} cos α sin α = \frac{1}{2} A B C = \frac{1}{4} A B \cdot A C sin α, \\ A N = \sqrt[]{\frac{A B_{0}}{2} \cdot A C} = \sqrt[]{A F \cdot A C} . \end{matrix}

3. Könnyen átvihetők eredményeink felezés helyett tetszőleges, 0 és 1 közti, szerkeszthető

λ

szám esetén a háromszöget

λ : (1 - λ)

arányban osztó egyenes kijelölésére.