Kezdőlap


Feladat:	F.1940	Korcsoport: 16-17	Nehézségi fok: -
Megoldó(k):	Alexy M. , Baranyi J. , Bárdossy Gy. , Bátyi L. , Borsodi D. , Brindza B. , Böősi I. , Dozmati Z. , Dózsa L. , Fehér J. , Frankó F. , Hajnal I. , Ható Mária , Hornung T. , Horváth Eszter , Horváth J. , Jakab T. , József S. , Kecskés Cs. , Kiss E. , Koltay K. , Kovács F. , Krausz T. , Krisztián T. , Lovász A. , Lux I. , Magyar L. , Miklós D. , Mikoss L. , Münnich Á. , Nagy Gábor (Kiskőrös) , Nagy János , Németh Gy. , Páles Zs. , Perge L. , Pintér Klára , Raikovich P. , Rapp F. , Réti Z. , Ságody Loránd , Sárga E. , Seress Á. , Sparing L. , Tokodi J. , Tornóci L. , Udvardy Magdolna , Varga B. , Vass A. (Debrecen)
Füzet:	1975/január, 15 - 16. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Szabályos sokszög alapú gúlák, Térfogat, Térgeometriai bizonyítások, Feladat
Hivatkozás(ok):	Feladatok: 1974/május: F.1940

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Áz állítást azzal bizonyíthatjuk be, hogy az $A' B' C D = T'$ tetraéder térfogata mindig $5 / 9$ része az $A B C D = T$ tetraéder térfogatának. Jelöljük az $A$ -val szemben levő $B C D$ lap súlypontját $S_{a}$ -val, az $A C D$ lap súlypontját $S_{b}$ -vel, a $C D$ él felezőpontját $F$ -fel. Így $F A$ , $F B$ az $A C D$ , illetve $B C D$ lap egyik-egyik súlyvonala, azért $S_{b}$ rajta van az $F A$ -n, $S_{a}$ pedig $F B$ -n, tehát $S_{b}$ , $S_{a}$ és a velük $B'$ és $A'$ is benne van az $F A B = Σ$ sí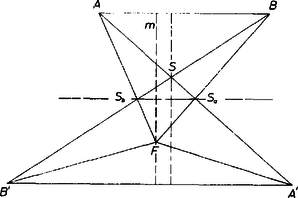kban.

Gondoljuk kettémetszve

T

-t is,

T'

-t is a

Σ

síkkal, a metszet az

F A B

, ill.

F' A' B'

háromszög. Az

F A B C

és

F A B D

tetraéderek térfogata egyenlő, mert alapsíknak a közös

F A B

lapjukat véve, magasságaik is egyenlők, hiszen

F

megválasztása folytán

C

és

D

egyenlő távolságra van

Σ

-tól, ennek két oldalán. Ugyanígy egyenlő

T'

két részének,

F A' B' C

-nek és

F A' B' D

-nek a térfogata is. És mivel e négy résznek a

Σ

-ra merőleges magasságai egyenlők, állításunk egyenértékű azzal, hogy az

F A' B'

alapháromszög területe egyenlő az

F A B

alapterületének

5 / 9

részével. Feladatunk ezáltal síkbeli feladattá egyszerűsödött.
Az

A S_{a}

és

B S_{b}

egyenesek

S

metszéspontja (ami egyébként a

T

súlypontja) negyedeli az

A S_{a}

B S_{b}

szakaszt, mert benne van az

A B S_{a} S_{b}

négyszögben, továbbá

F S_{b} : F A = F S_{a} : F B = 1 : 3

alapján

S_{a} S_{b} | | A B

és

S_{a} S_{b} = A B / 3

, az

S S_{a} S_{b}

háromszög

1 / 3

arányú kicsinyített képe az

S A B

háromszögnek,

S S_{a} = S A / 3

. Továbbmenve

S A' = S S_{a} + S_{a} A' = S S_{a} + S_{a} A = S S_{a} + 4 S S_{a} = 5 S S_{a}

, és ugyanúgy

S B' = 5 S S_{b}

; ezért

A' B' | | S_{a} S_{b} | | A B

, és

A' B' = 5 S_{a} S_{b} = 5 A B / 3

.
Az

F A B

háromszög

F

-ből húzott magasságát

m

-mel jelölve

F

és

S

távolsága az

S_{a} S_{b}

egyenestől (ennek két oldalán)

\frac{m}{3}

, illetve

\frac{1}{4} \cdot \frac{2 m}{3} = \frac{m}{6}

, tehát az

A' B'

egyenestől az

S

pont

\frac{5 m}{6}

, az

F

pont pedig

\frac{5 m}{6} - \frac{m}{6} - \frac{m}{3} = \frac{m}{3}

távolságra van.

Így az

A' B' F

háromszög területe:

\begin{matrix} \frac{1}{2} \frac{5 A B}{3} \cdot \frac{m}{3} = \frac{5}{9} \cdot \frac{A B m}{2} \end{matrix}

Állításunkat bebizonyítottuk, ez pedig tartalmazza a feladat állítását, hiszen

5 / 9 > 1 / 2