Kezdőlap


Feladat:	F.1939	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Bagó B. , Balassa A. , Bárdossy Gy. , Bezdek A. , Brindza B. , Böősi I. , Dózsa L. , Fehér J. , Forgács I. , Frankó F. , Hornung T. , Jakab T. , Kecskés Cs. , Kiss E. , Koltay K. , Kovács Imre , Krausz T. , Mercz B. , Münnich Á. , Nagy Gábor (Kiskőrös) , Nagy János , Páles Zs. , Pintér Klára , Sárga E. , Sparing L. , Varga B. , Varga L. (Debrecen) , Vass A (Debrecen)
Füzet:	1981/november, 118 - 119. oldal		PDF \| MathML
Témakör(ök):	Térelemek és részeik, Feladat
Hivatkozás(ok):	Feladatok: 1974/május: F.1939

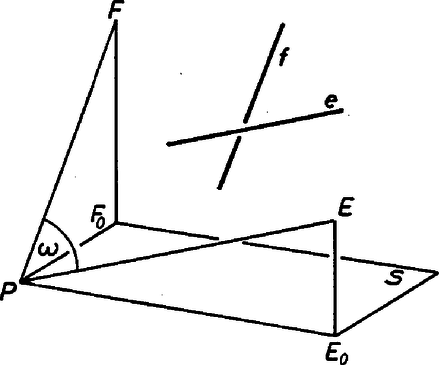
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $P$ az $S$ és $T$ síkok metszésvonalának tetszőleges pontja, és legyenek $E$ , $F$ olyan pontok a térben, amelyekre $P E$ az $e$ -vel, $P F$ az $f$ -fel párhuzamos, továbbá a $P E$ , $P F$ szakaszok hossza egységnyi. Azt fogjuk megmutatni, hogy az $ω = E P F$ szögre

\begin{matrix} | cos ω | \leq 1 / 3 \end{matrix}

(1)

teljesül, amiből következik a feladat állítása.

Jelöljük az

E

F

pontok

S

-en levő vetületét

E_{0}

-lal,

F_{0}

-lal, akkor a feladat szerint

E_{0} P

merőleges

F_{0} P

-re, Először a koszinusz tételt, majd Pitagorasz tételét alkalmazva kapjuk, hogy

\begin{matrix} E F^{2} & = 2 - 2 cos ω = E_{0} F_{0}^{2} + {(E_{0} E - F_{0} F)}^{2} = (P E_{0}^{2} + E_{0} E^{2}) + (P F_{0}^{2} + F_{0} F^{2}) - 2 E_{0} E \cdot F_{0} F = 2 - 2 E_{0} E \cdot F_{0} F, \end{matrix}

ahol az

E_{0} E

F_{0} F

távolságokat előjelesen értjük: egyező az előjelük, ha egyirányúak. A két összefüggésből adódik, hogy

\begin{matrix} cos ω = E_{0} E \cdot F_{0} F . \end{matrix}

(2)

Vezessünk be térbeli koordináta-rendszert úgy, hogy annak

P

legyen az origója, az

y

tengely

S

és

T

metszésvonalán legyen, az

x

tengely

S

-ben, a

z

tengely

T

-ben, és jelöljük

E

F

koordinátáit

(e_{1}; e_{2}; e_{3})

-mal, illetve

(f_{1}; f_{2}; f_{3})

-mal. Akkor

\begin{matrix} \sum_{i = 1}^{3} e_{i}^{2} = \sum_{i = 1}^{3} f_{i}^{2} = 1, \end{matrix}

(3)

és

(2)

-t először változtatás nélkül, majd

S

és

T

szerepének felcserélésével alkalmazva kapjuk, hogy

\begin{matrix} e_{3} f_{3} = e_{1} f_{1} = cos ω \end{matrix}

(4)

(x; y)

síkban az

E_{0}

F_{0}

pontok koordinátái

(e_{1}; e_{2})

, illetve

(f_{1}; f_{2})

, így ismét az

E_{0} F_{0} P

derékszögű háromszögben alkalmazva Pitagorasz tételét, kapjuk, hogy

\begin{matrix} {(e_{1} - f_{1})}^{2} + {(e_{2} - f_{2})}^{2} = (e_{1}^{2} + e_{2}^{2}) + (f_{1}^{2} + f_{2}^{2}), \end{matrix}

vagyis

\begin{matrix} e_{1} f_{1} + e_{2} f_{2} = 0. \end{matrix}

(5)

(4)

és

(5)

alapján látható, hogy

cos ω

értéke

- e_{2} f_{2}

-vel is egyenlő,

(1)

tehát következik a

\begin{matrix} | e_{1} f_{1} - e_{2} f_{2} + e_{3} f_{3} | \leq 1 \end{matrix}

(6)

egyenlőtlenségből, hiszen esetünkben a bal oldalon álló három mennyiség egyenlő.
Így már csak

(6)

igazolása van hátra. Legyen még

g_{1} = e_{1}

g_{2} = - e_{2}

g_{3} = e_{3}

, akkor

(6)

a nevezetes

\begin{matrix} {(\sum_{i = 1}^{3} f_{i} g_{i})}^{2} \leq \sum_{i = 1}^{3} f_{i}^{2} \sum_{i = 1}^{3} g_{i}^{2} \end{matrix}

(7)

egyenlőtlenség alapján következik

(3)

-ból. A

(7)

egyenlőtlenség legegyszerűbben annak alapján látható be, hogy a

\begin{matrix} \sum_{i = 1}^{3} {(f_{i} - t g_{i})}^{2} = \sum_{i = 1}^{3} f_{i}^{2} - 2 t \sum_{i = 1}^{3} f_{i} g_{i} + t^{2} \sum_{i = 1}^{3} g_{i}^{2} \end{matrix}

másodfokú polinom értéke minden valós

t

mellett nem negatív, így a diszkriminánsa nem lehet pozitív.

Megjegyzés. Ha megoldásunk elején nem alkalmaztuk volna a Pitagorasz tételt, azt kaptuk volna, hogy

\begin{matrix} cos ω = \sum_{i = 1}^{3} e_{i} f_{i} . \end{matrix}

Szokás a jobb oldalon álló mennyiséget az

(e_{1}; e_{2}; e_{3})

(f_{1}; f_{2}; f_{3})

vektorok skaláris szorzatának nevezni. A név arra utal, hogy bár vektorokat szorzunk össze, az eredmény szám, skaláris mennyiség. Jól látható itt a szorzás fogalmánek kettős tulajdonsága: van amikor két mennyiség szorzata ugyanolyan típusú mennyiség, mint a szorzandók, és van, hogy a szorzat a mennyiségek típusától függetlenül egyetlen, a mennyiségek viszonyát kifejező valós szám. Az utóbbi esetben ha a szorzat értéke

0

, szokás egymásra merőlegesnek mondani a mennyiségeket, hiszen két és három dimenzióban így épp azokat a vektorokat mondjuk merőlegeseknek, amelyek geometriai értelemben is merőlegesek.