Kezdőlap


Feladat:	F.1938	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Alexy M. , Baranyai J. , Bárdossy Gy. , Bezdek A. , Borsodi D. , Böősi I. , Csapó Gy. , Fehér J. , Forgács I. , Gyarmati P. , Hornung T. , Horváth Árpád , Horváth Eszter , Horváth Z. , Kecskés Cs. , Kiss E. , Koltay K. , Kovács Éva , Krausz T. , Nagy Gábor (Kiskőrös) , Nagy János , Páles Zs. , Perge L. , Rács Ágnes , Rapp F. , Seress Á. , Sparing L. , Süvöltős F. , Szűcs Gy. , Tokodi J. , Torma T. , Török K. , Udvardy Magdolna , Varga Z. (Debrecen) , Vass A. (Debrecen)
Füzet:	1975/január, 12 - 15. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Terület, felszín, Trapézok, Síkgeometriai szerkesztések, Síkbeli szimmetrikus alakzatok, Szabályos sokszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1974/május: F.1938

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az ötszög csúcsait $A$ , $B$ , $C$ , $D$ , $E$ -vel, az ötszög területét $T$ -vel, és keressük az $A B$ -vel párhuzamos terület-negyedelőket. Legyen $C_{0}$ a $C$ csúcs $A E$ -en levő vetülete, $C C_{0}$ felezi az ötszög területét, hiszen szimmetriatengelye. Emiatt az $A B C E$ trapéz területe nagyobb $T / 2$ -nél, a területfelező ebben a trapézban halad. Jelöljük a $B C$ , $A E$ egyenesek metszéspontját $D_{1}$ -gyel, és vegyük hozzá az $A B C C_{0}$ négyszöghöz az $A B D_{1}$ háromszöget, kapjuk a $C C_{0} D_{1}$ derékszögű háromszöget. Ha sikerül olyan, ezzel egyenlő területű, egyenlő szárú háromszöget szerkesztenünk, amelyiknek a szárai az $A D_{1}$ , $B D_{1}$ egyenesek, meg is van a területfelező egyenes. Valóban, ha ebből az egyenlő szárú háromszögből elvesszük az $A B D_{1}$ , háromszöget, a visszamaradó trapéz területe épp $T / 2$ lesz, hiszen egyenlő $A B C C_{0}$ területével.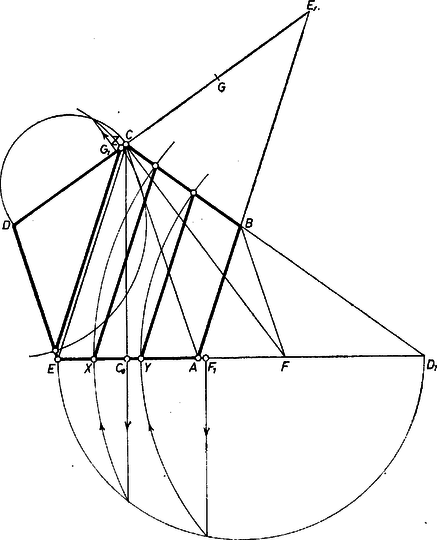

Jelöljük a területfelező egyenes

A E

-vel alkotott metszéspontját

X

-szel.
A mondott egyenlő szárú háromszög területe egyrészt

\frac{1}{2} D_{1} X^{2} sin 36^{\circ}

, másrészt

\frac{1}{2} C_{0} D_{1} \cdot C D_{1} \cdot sin 36^{\circ}

, tehát a

D_{1} X

szakasz egyenlő a

D_{1}

D_{1} C_{0}

szakaszok mértani közepével. A szokásos eljárást követve rajzoljunk

E D_{1}

fölé Thalész-kört, ennek a

C C_{0}

egyenesen levő pontját forgassuk le

D_{1}

körül a

D_{1} E

egyenesre, kapjuk

X

-et.
Jelöljük a most megszerkesztett trapéz területét felező,

A B

-vel párhuzamos egyenes

A E

-n levő pontját

Y

-nal: ez határozza meg az ötszög egyik keresett területnegyedelőjét. Az egyszer már alkalmazott gondolatmenetet követve először olyan háromszöget keresünk, amelynek oldalai az

E D_{1}

C D_{1}

egyenesek, és amelyiknek területe egyenlő

T / 4

-nek és az

A B D_{1}

háromszög területének az összegével. Ehhez csak el kell vennünk

C_{0} C D_{1}

-ből egy

T / 4

területű darabot. Húzzunk párhuzamost

B

-n át

A C

-vel, és messe ez

A D_{1}

-et

F

-ben. Az

A B C

A F C

háromszögek területe egyenlő, tehát

C C_{0} F

területe egyenlő

A B C C_{0}

területével, vagyis

T / 2

-vel. Legyen a

C_{0} F

szakasz felezőpontja

F_{1}

, ekkor

C F_{1} D_{1}

a keresett háromszög, és

D_{1} Y

egyenlő

D_{1} C

és

D_{1} F_{1}

mértani közepével.

Y

-t tehát megkapjuk, ha az imént használt Thalész-kör

F_{1}

feletti pontját

D_{1}

körül leforgatjuk

E D_{1}

-re.
A harmadik egyenes a

C D E

háromszöget vágja ketté, hiszen (mint azt hamarosan belátjuk),

C E

C_{0} C D E

idomot úgy vágja ketté, hogy a keletkezett darabok közül

C D E

a nagyobb területű. Jelöljük ennek a területnegyedelőnek

C D

-n levő pontját

Z

-vel. Most a

D E

D C

szárakra fogunk

T / 4

területű háromszöget helyezni. Tükrözzük

E

-t

B C

-re, kapjuk

E_{1}

-et. Könnyen igazolhatjuk, hogy az

A

B

E_{1}

pontok, valamint a

C

D

E_{1}

pontok egy egyenesen vannak. A

B E_{1} C E

rombusznak

B C E

is,

C E E_{1}

is fele, ezek tehát egyenlő területűek. Jelöljük

C E_{1}

felezőpontját

G

-vel,

C E G

területe egyenlő

C C_{0} E

területével, tehát

D E G

területe

T / 2

. Legyen

D G

felezőpontja

G_{1}

, a keresett

D Z

szakasz

D G_{1}

és

D C

mértani közepe, hiszen

D E G_{1}

területe

T / 4

. Ezek szerint a

C D

feletti Thalész-kör

G_{1}

feletti pontját kell

D

körül

C D

-re leforgatnunk, kapjuk

Z

-t.
Be kell még látnunk, hogy az így megszerkesztett

Z

valóban a

C D

szakaszon van. Elég belátnunk, hogy

D G_{1} < D C

, vagyis

D G < 2 C D

C D > C G

2 C D > C E_{1} = C E

, és itt a legutolsó egyenlőtlenség nem más, mint a

C D E

háromszögre vonatkozó

C E < C D + D E

háromszög-egyenlőtlenség.

Megjegyzések. 1. Ha az ötszög oldalát választjuk egységnek, és az átló hosszát

a

-val jelöljük, akkor megoldásunk szerint

\begin{matrix} D_{1} X^{2} = (1 + a) (\frac{1}{2} + a) = \frac{1}{2} + \frac{3}{2} a + a^{2} . \end{matrix}

A B D_{1}

E C D_{1}

háromszögek hasonlósága alapján

\begin{matrix} 1 : a = a : (1 + a), \end{matrix}

tehát

a^{2} = 1 + a

a = \frac{1 + \sqrt[]{5}}{2}

, és

\begin{matrix} D_{1} X^{2} = \frac{3}{2} + \frac{5}{2} a = \frac{11 + 5 \sqrt[]{5}}{4}, \\ A X = \frac{\sqrt[]{11 + 5 \sqrt[]{5}} - (\sqrt[]{5} + 1)}{2} = 0, 74. \end{matrix}

Mivel

\begin{matrix} A F : A D_{1} = C B : C D_{1}, A F = \frac{a}{a + 1} = a - 1, F D_{1} = 1, F_{1} D_{1} = \frac{1}{2} (1 + \frac{1}{2} + a), \end{matrix}

és így

\begin{matrix} D_{1} Y^{2} = (1 + a) \frac{2 a + 3}{4} = \frac{2 a^{2} + 5 a + 3}{4} = \frac{7 a + 5}{4} = \frac{17 + 7 \sqrt[]{5}}{8} . \\ A Y = \frac{\frac{1}{2} \sqrt[]{34 + 14 \sqrt[]{5}} - (\sqrt[]{5} + 1)}{2} = 0, 40. \end{matrix}

Végül

\begin{matrix} D G_{1} = \frac{1}{2} D G = \frac{2 + a}{4} = \frac{5 + \sqrt[]{5}}{8}, \\ D Z = \frac{\sqrt[]{10 + 2 \sqrt[]{5}}}{4} = 0, 95. \end{matrix}

Természetesen ezeket a számokat a feladat követelményei alapján felírható egyenletekből is meghatározhatjuk. Ebben az esetben a kapott eredményeket azonban még valahogy meg kell szerkesztenünk.

2. Az ábra azt mutatja, hogy a területfelező egyenes közel van az ötszög centrumához. Az olvasóra bízzuk annak meggondolását, miért kell a területfelezőnek közel lennie a centrumhoz, és miért nem megy át pontosan rajta.