Kezdőlap


Feladat:	F.1935	Korcsoport: -	Nehézségi fok: -
Megoldó(k):	Jakab Tibor
Füzet:	1981/március, 97 - 104. oldal		PDF \| MathML
Témakör(ök):	Kombinatorikai leszámolási problémák, Feladat
Hivatkozás(ok):	Feladatok: 1974/május: F.1935

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük $P$ elemeit $1 \leq i \leq 7$ mellett $P_{i}$ -vel, ekkor $C$ elemei egyrészt a $P_{i}^{2}$ négyzetszámok lesznek $1 \leq i \leq 7$ mellett, másrészt a $P_{i} P_{j}$ alakú szorzatok $1 \leq i \leq j \leq 7$ mellett. A keresett felbontások egy‐egy részhalmazába pontosan egy négyzetszámnak kell kerülnie, hiszen két négyzetszámhoz, mondjuk $P_{1}^{2}$ -hez és $P_{2}^{2}$ -hez $C$ elemei között csak egy olyan található, amelyik egyikhez sem relatív prím, a $P_{1} P_{2}$ szorzat. Emiatt a részhalmazok azonosíthatóak a bennük levő négyzetszámokkal.
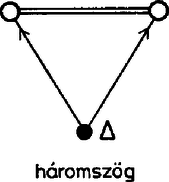
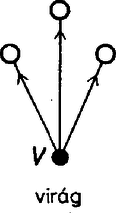
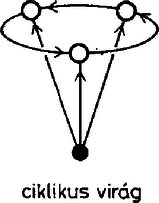
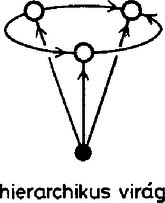
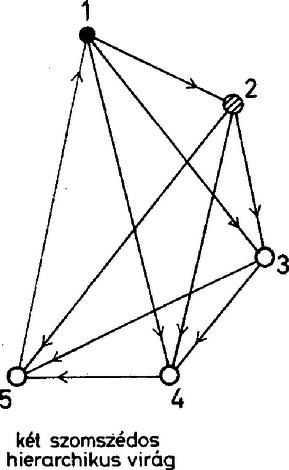
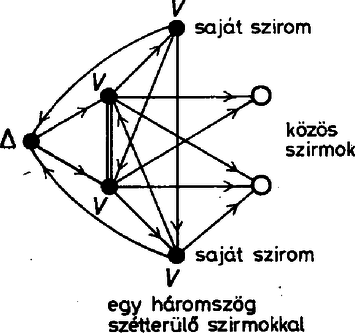
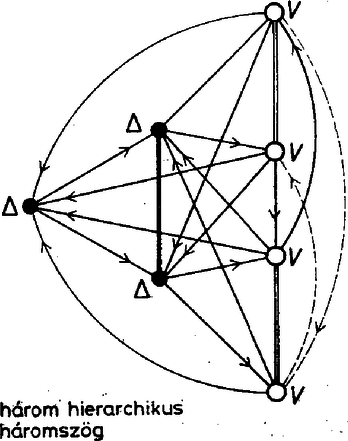
Szemléletesebben le tudjuk írni a keresett felbontásokat, ha pontokkal ábrázoljuk a $P$ halmaz elemeit, és a $C$ halmaz $P_{i} P_{j}$ alakú elemeinek a $P_{i}$ , $P_{j}$ pontokat összekötő vonalakat (éleket) feleltetünk meg. Ezt a 21 vonalat kell hét csoportba osztani úgy, hogy mindegyik csoport egy‐egy ponthoz tartozzon. A feladat kitöltései szerint a $P_{i}^{2}$ -et tartalmazó részhalmazba $C$ -ből legalább két $P_{i}$ -vel osztható elemnek kell kerülnie. Ha ezek ‐ mondjuk ‐ a $P_{i} P_{j}$ , $P_{i} P_{k}$ szorzatok, ahol $i$ , $j$ , $k$ különbözőek, akkor a negyedik elem vagy a $P_{j} P_{k}$ szorzat, vagy ez is osztható $P_{i}$ -vel, hiszen ennek is legalább kettővel kell közös törzstényezőt tartalmaznia a másik három elem közül.

A választott szemléltetésünkben ez azt jelenti, hogy a

P_{i}

ponthoz választandó három él közül kettőnek

P_{i}

-ből kell indulnia, a harmadiknak pedig vagy ezek második végpontjait kell összekötnie, vagy annak is

P_{i}

-ből kell indulnia. Nevezzük az utóbbi konfigurációt virágnak és jelöljük

V

-vel, az előbbit pedig háromszögnek és jelöljük

Δ

-gel. Ábráinkon a virágok éleit közös csúcsukból kifelé mutató nyilakkal látjuk el, a háromszögnél csak a

P_{i}

csúcsból kiinduló éleket irányítjuk, és a harmadik élt kettős vonallal rajzoljuk meg, hogy fokozatosan épülő konstrukcióinkban mindig tudjuk, melyik él sorsáról döntöttünk már és hogyan. Ugyancsak ennek érdekében a foglalt csúcsokat fekete kör, a szabadokat fehér kör fogja jelölni. ‐ A csúcsok és a prímek megfeleltetéséről általában csak a konstrukció befejezése után döntünk. A lehetséges eseteket a háromszögek száma szerint vesszük sorra.
Először azokat a felbontásokat számoljuk össze, amelyekben csupa virág szerepel. Most így szól a feladatunk: adott hét város, és bármelyik kettő között egy út. Hányféleképpen tehetjük egyirányúvá az utakat, ha minden városból pontosan háromnak kell kifutnia? A három kifutó út alkotja a virágot, a kiindulási város a virág töve, a másik három város a virág szirma. Vegyünk egy virágot, és nézzük meg a szirmai közti utak irányítását. Csak kétféle eset lehetséges: a szirmok közti három út mentén vagy tehetünk körutat, vagy nem. Az első esetben ciklikusnak mondjuk a virágot, a másodikban hierarchikusnak. Ez utóbbinak a szirmai ugyanis egyértelműen sorba rendezhetők úgy, hogy köztük mindig a sorban elöl állóból fut az út a hátul álló felé. Maga a tő is beilleszthető ebbe a sorba, egyszerűen legelőlre kell tenni.
Vegyünk egy hierarchikus virágot, állítsuk sorba a benne szereplő négy várost, és vizsgáljuk meg az első sziromból eredő virág típusát. Vegyük először azt az esetet, amikor ez a virág is hierarchikus. Ekkor ennek a virágnak a harmadik szirma folyamatosan csatlakozik az első virág által kialakított hierarchiához, az ott létrejövő sor végére illeszthető. Most már öt város szerepel a konstrukcióban, és a köztük futó 10 út irányítása közül csak egynek az irányítása tér el a hierarchiától. A legelső és legutolsó város közti út irányítása ugyanis csak fordított lehet, hiszen az első városból kifutó éleket már ismerjük, a még nem irányított többi út csak befelé futhat ebbe a városba.

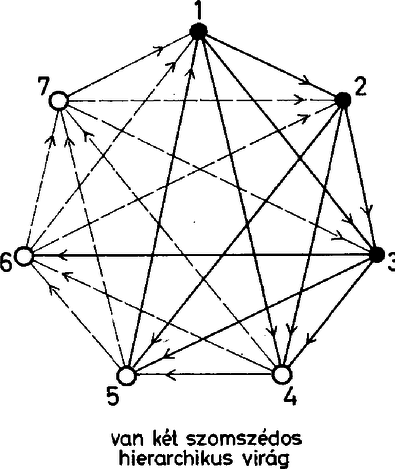
A városok között kialakuló hierarchia tehát nem nagyon erős, a negyed‐szomszédra már nem érvényes. Térjünk rá a harmadik város vizsgálatára, és helyezzük eleve a sor végére hatodiknak az ebből eredő virág harmadik szirmát. Mivel a sor negyedik és ötödik városába már megvan a három befutó utunk, a további utak azokból csak kifelé indulhatnak. Ez azt jelenti, hogy két szomszédos hierarchikus virág töve mögött a harmadik város már csak hierarchikus virág töve lehet. Innen most már egyértelműen körbeszaladhatunk a városainkon: mivel a sor második és harmadik eleme hierarchikus, csak az lehet a negyedik elem is, és így tovább. Mind a hét város hierarchikus, és ez a sorrend az összes út irányítását egyértelműen meghatározza. (Azt is látjuk, miért fut 5-ből 1-be az út, és nem megfordítva, hiszen 6-on és 7-en át előbb jutunk 5-ből 1-be, mint 2-n, 3-on, 4-en át 1-ből 5-be.)
Az elmondottak alapján már meg tudjuk határozni azoknak az irányításoknak a számát, amelyekben van két szomszédos hierarchikus virág. Mint láttuk, annyi ez, ahányféle körutat tehetünk a hét városban. Utunk kezdő városát tetszés szerint választhatjuk: ez nem jellemző az útra, hiszen ide is vissza kell jutnunk. A második állomás 6-féleképpen, a harmadik 5-féleképpen, a negyedik 4-féleképpen, az ötödik 3-féleképpen, a hatodik 2-féleképpen választható meg, és a hetedik már egyértelmű. A lehetőségek száma tehát

6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 6! = 720

.
Álljunk itt meg egy pillanatra! A szabályos hétszögben háromféle szakasz található, a hétszög oldala, egy rövidebb és egy hosszabb átló. Ezekből háromféle körút alakítható ki, ha egy körúthoz csak egyféle szakaszt használunk.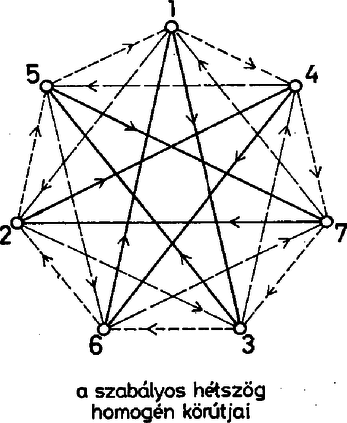

Mindhárom körút kétféle irányban járható be, ha tehát az oldalak bejárását az óramutató járása szerintinek választjuk, ehhez képest a másik két körút irányítására négy lehetőségünk marad. A négy közül egyet már ismerünk, ez az, amit két szomszédos hierarchikus virágból kapunk. Ha ebben ‐ mondjuk ‐ a rövidebb átlók irányítását megfordítjuk, változatlanul minden csúcsból három él fut ki, és ezek továbbra is hierarchikus virágot alkotnak. Biztos, hogy ezt az elrendezést számba vettük az előbb? Hát persze, csak most a körutat a rövidebb átlók mentén kell tenni, és eszerint kell sorba állítani a csúcsokat.

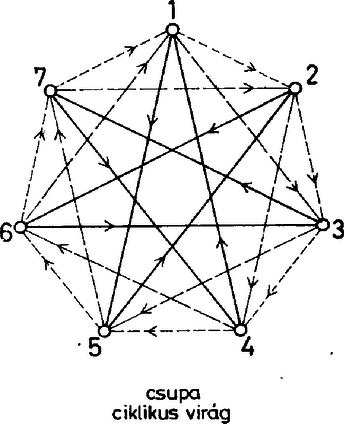
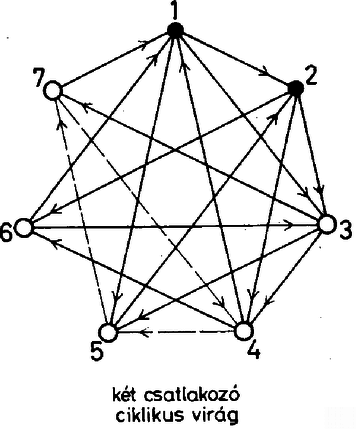
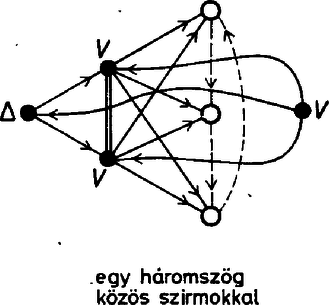
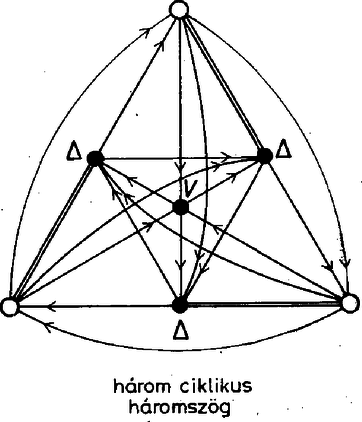
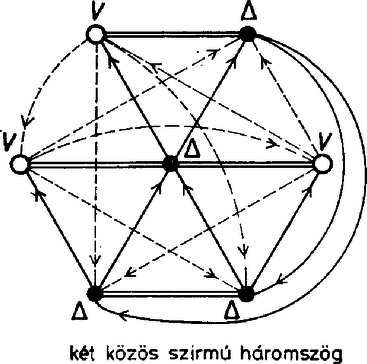
Más lesz a helyzet, ha a hosszabb átlók irányítását fordítjuk meg, mert ennek hatására minden virág ciklikussá válik. Ugyanezt a konstrukciót kapjuk, ha benne első körútnak a rövidebb vagy a hosszabb átlók által alkotott csillagot választjuk, a mindenkori első úthoz viszonyított második út irányítása megegyezik az első útéval, a harmadiké fordított. Emiatt most az összes esetre az előbb kapott számot még hárommal el kell osztani, csak 240 olyan irányítás van, amelyikben minden virág ciklikus.

Meg kell még mutatnunk, hogy csak a talált módon kapható olyan irányítás, amelyikben minden virág ciklikus. Vegyünk egy tetszés szerinti virágot, és számozzuk meg a tövét 1-essel, az egyik szirmát 2-essel, az ebből elérhető szirmot 3-assal, a harmadik szirmot 5-össel. Most térjünk rá a 2-es csúcsból eredő virágra, ennek a 3-as csúcs szirma, az 1-es és 5-ös nem. A két másik szirom tehát új csúcs, közülük a 3-ból elérhető legyen a 4-es, a másik a 6-os. Most már a 3-as tövű virág egyértelmű, hisz ennek csak 4, 5 és a még fel nem vett 7 lehet a szirma, köztük a körbejárás abból adódik egyértelműen, hogy a 4 tövű ciklikus virágnak 1 és 6 biztosan szirma, és ezek mellett 5 és 7 közül csak 5 lehet a harmadik szirom, hiszen 6-ból is, 7-ből is 1 felé fut az út. Innen kezdve könnyen befejeződik a konstrukció: 5-be már fut be három él, tehát 5-ből 6 felé kell menni, ezután 6-ból csak 7 felé mehetünk, és 7-ben is megvan a három befutó él. Ezzel beláttuk, hogy ha minden virág ciklikus, háromféle körút alakítható ki a csúcsokból az irányítás mentén. (A három lehetőség a legelső virág szirmainak a számozásában tér el egymástól.)

Térjünk most vissza eredeti gondolatmenetünkre. Vizsgálódásainkat azzal kezdtük, hogy vettünk egy hierarchikus virágot, és beláttuk, hogy ha ennek a hierarchia szerinti első szirma is hierarchikus virág töve, akkor minden virág hierarchikus. Mivel közben a csupa ciklikus virágokat tartalmazó irányításokat összeszámoltuk, már csak azt az esetet kell megvizsgálnunk, amikor van hierarchikus virág, de annak az első szirma ciklikus virág töve. Ennek a virágnak két szirma már ismert, ezek az első virágbeli szirom‐társak, viszont a harmadik szirom csak újabb csúcs lehet. Mivel ez a virág ciklikus, a szirmai közti irányítást az első két szirom közti út irányítása egyértelműen meghatározza. Azt kapjuk, hogy az első virág másik két szirmába a már irányítottak közül három‐három fut be, ezekből tehát a többi már csak kifelé futhat.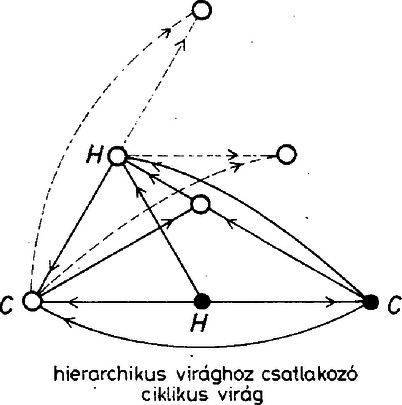

Azt is látjuk, hogy a második sziromból eredő virág hierarchikus, és ennek első szirma éppen az első virág harmadik szirma. Gondolatmenetünk ettől kezdve ciklikusan megismételhető. Végül is három hierarchikus virágot kapunk, és a négy ciklikus virág közül az egyik kitüntetett szerepű, ennek épp a hierarchikus virágok tövei a szirmai. Az egyes csúcsokhoz a hét prímszám 7 !-féleképpen rendelhető hozzá, de mivel a konfigurációt a centrális helyzetű ciklikus virág töve körül elforgathatjuk, a különböző esetek száma ennek harmada,

7! / 3 = 1680

Rátérünk azoknak az eseteknek a vizsgálatára, amikor egy háromszög van. Vigyük át a virágokra vonatkozó elnevezéseinket a háromszögekre is, mondjuk a háromszög első csúcsát annak tövének, a másik kettőt pedig sziromnak. Ha csak egy háromszög van, annak szirmai csak virágok tövei lehetnek, és ezek szirmai a többi 4 csúcs közül kerülnek ki. Két eset lehetséges: e két virágnak vagy mindhárom szirma közös, vagy nem. Az utóbbi esetben mindkét virágnak van egy‐egy saját szirma, de két szirmuk ekkor is közös.

Ennek a konstrukciónak a befejezését a két saját és a két közös szirom közti utak irányítása már egyértelművé teszi (az ábrán lefelé). Mivel a konstrukcióban minden csúcs szerepe más, az esetek száma

7! = 5040

Ha a háromszög szirmaiból eredő virágok szirmai közösek, a hetedik csúcsból eredő virágnak csak a háromszög csúcsai lehetnek a szirmai. Ezután a konstrukció már egyértelműen fejezhető be, és benne a 3 közös szirom és a háromszög szirmai egymástól függetlenül ciklikusan felcserélhetők. A különböző esetek száma emiatt csak az előbbiek hatoda,

7! / 6 = 840

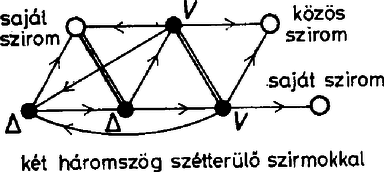
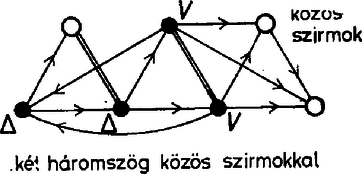
Ha két háromszög van, a tövüket összekötő él csak az egyikükhöz tartozhat, vagyis az egyiknek a töve a másik háromszögnek szirma. Ennek a szirmaiból virágok nőnek, amelyekre változatlanul érvényesek az előző esetben mondottak, de az első háromszög töve csak közös szirom lehet. A szétterülő szirmok esetében ismét minden csúcs szerepe más, tehát

7! = 5040

eset van. A közös szirmok esetében az első háromszög jelenléte megkülönbözteti a közös szirmok szerepét, tehát az esetek száma

7! / 2 = 2520

.
Ha három háromszög van, közülük kettőnek a töve a harmadik háromszögnek szirma lehet, vagy pedig ciklikusan egymás szirmai lesznek a töveik. Az első esetet most is hierarchikusnak, a másodikat ciklikusnak nevezzük. A hierarchikus esetben az első szirmaiból eredő két háromszög négy szirma csak a még fel nem használt 4 csúcs lehet. (Nem lehet közös szirom, mert abból már nem eredhetne virág.) Különben a 4 új csúcs ciklusba rendeződik, és ezen belül páronként felcserélhetők. Emiatt az összes eset száma 7 ! negyede, vagyis 1260.
Ha a három háromszög ciklikusan csatlakozik egymáshoz, további szirmaikkal együtt hat pontot határoznak meg. A hetedikből virág ered, és ennek csak a háromszögek tövei lehetnek a szirmai. Ez a pont a másik három virágnak közös szirma, továbbá mindegyiknek még egy háromszög töve a szirma és ciklikusan egymás szirmai. A hét csúcshoz a hét prímszám 7 !-féleképpen rendelhető hozzá, de a konstrukció forgásszimmetriája miatt ennek csak harmada a különböző esetek száma. Azonban az utak minden konkrét hozzárendelés mellett kétféleképpen irányíthatóak, hiszen a háromszögek és a virágok töveinek ciklusa egyirányú is lehet egymással és ellentétes irányításúak is lehetnek. A különböző irányítások száma tehát

2 \cdot 7! / 3 = 3360

.
Ha négy vagy több háromszög szerepel a konstrukcióban, ezeknek már biztosan van közös szirmuk. Ha két háromszögnek van közös szirma, más csúcs bennük nem lehet közös, tehát együtt öt pontot határoznak meg.

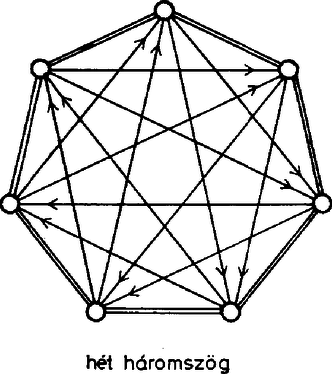
Emiatt a közös sziromból már csak háromszög eredhet, hiszen ennek csak a két fel nem használt csúcs lehet a szirma. Az első két közös szirmú virág töve viszont csak egy újabb háromszög szirma lehet, amelynek a töve csak a harmadik háromszög szirmai közül választható. Ha pontosan négy háromszög van, az ábra egyértelműen fejezhető be, és a különböző esetek száma

7! = 5040

Háromnál kevesebb virág csak úgy lehet, ha egyáltalán nincs virág, mert egy virág tövének legalább egy másik virágban sziromnak kell lennie, hiszen a virágok tövéből páratlan sok él indul, a háromszögeknek viszont minden csúcsában páros sok él szerepel, és eredetileg minden csúcshoz összesen páros sok él tartozik. Emiatt ha két háromszög szerepel a konstrukcióban, minden csúcs pontosan két háromszög szirma. A szirmok mentén tehát körút tehető, elvileg azonban még előfordulhatna, hogy két külön körút alakul ki, egy négyelemű és egy háromelemű. Ez azért nem lehetséges, mert a négyelemű körút négy szirompárjához csak a köztük nem szereplő csúcsok jöhetnek szóba tőnek. Ha a szirmok mentén hételemű körút tehető, helyezzük azokat ebben a sorrendben egy szabályos hétszög csúcsaiba. A háromszögek szárai a sokszög 14 átlója közül kerülnek ki. Mindegyikben kell rövidebb és hosszabb átlónak is szerepelnie, mert két hosszabb átlóból ugyan alkotható háromszög, de ha ilyen szerepelne a 7 háromszög között, akkor olyannak is kellene szerepelnie, amelyikben két rövidebb átló kerül össze. Így ha a hétszög körüljárását is figyelembe vesszük, a konstrukció egyértelmű, és a különböző esetek száma

6! = 720

.
Eredményeinket a következő táblázatban foglaljuk össze. Az összes eset száma eszerint

26 460

\begin{matrix} A három- \\ szögek & Típus & Az esetek száma \\ száma \\ 0 & Van két szomszédos hierarchikus virág & \begin{matrix} 6! = 720 \\ \frac{6!}{3} = 240 \\ \frac{7!}{3} = 1680 \end{matrix}} 2640 \\ Csupa ciklikus virág \\ Kevert tipus \\ 1 & Egy háromszög szétterülő szirmokkal & \begin{matrix} 7! = 5040 \\ \frac{7!}{6} = 840 \end{matrix}}5840 \\ Egy háromszög közös szirmokkal \\ 2 & Két háromszög szétterülő szirmokkal & \begin{matrix} 7! = 5040 \\ \frac{7!}{2} = 2520 \end{matrix}}7560 \\ Két háromszög közös szirmokkal \\ 3 & Három hierarchikus háromszög & \begin{matrix} \frac{7!}{4} = 1260 \\ \frac{2 \cdot 7!}{3} = 3360 \end{matrix}}4620 \\ Három ciklikus háromszög \\ 4 & - & 7! = 5040 \\ 7 & - & 6! = 720 \\ 0-7 & Együttvéve & \frac{21 \cdot 7!}{4}=26 460 \end{matrix}

Jakab Tibor (Budapest, Berzsenyi D. Gimn.)